

تاريخ الرياضيات

الاعداد و نظريتها

تاريخ التحليل

تار يخ الجبر

الهندسة و التبلوجي


الرياضيات في الحضارات المختلفة

العربية

اليونانية

البابلية

الصينية

المايا

المصرية

الهندية


الرياضيات المتقطعة

المنطق

اسس الرياضيات

فلسفة الرياضيات

مواضيع عامة في المنطق


الجبر

الجبر الخطي

الجبر المجرد

الجبر البولياني

مواضيع عامة في الجبر

الضبابية

نظرية المجموعات

نظرية الزمر

نظرية الحلقات والحقول

نظرية الاعداد

نظرية الفئات

حساب المتجهات

المتتاليات-المتسلسلات

المصفوفات و نظريتها

المثلثات


الهندسة

الهندسة المستوية

الهندسة غير المستوية

مواضيع عامة في الهندسة

التفاضل و التكامل


المعادلات التفاضلية و التكاملية

معادلات تفاضلية

معادلات تكاملية

مواضيع عامة في المعادلات


التحليل

التحليل العددي

التحليل العقدي

التحليل الدالي

مواضيع عامة في التحليل

التحليل الحقيقي

التبلوجيا

نظرية الالعاب

الاحتمالات و الاحصاء

نظرية التحكم

بحوث العمليات

نظرية الكم

الشفرات

الرياضيات التطبيقية

نظريات ومبرهنات


علماء الرياضيات

500AD

500-1499

1000to1499

1500to1599

1600to1649

1650to1699

1700to1749

1750to1779

1780to1799

1800to1819

1820to1829

1830to1839

1840to1849

1850to1859

1860to1864

1865to1869

1870to1874

1875to1879

1880to1884

1885to1889

1890to1894

1895to1899

1900to1904

1905to1909

1910to1914

1915to1919

1920to1924

1925to1929

1930to1939

1940to the present

علماء الرياضيات

الرياضيات في العلوم الاخرى

بحوث و اطاريح جامعية

هل تعلم

طرائق التدريس

الرياضيات العامة

نظرية البيان
Five Candidates, Five Winners
المؤلف:
W.D. Wallis
المصدر:
Mathematics in the Real World
الجزء والصفحة:
194-196
14-2-2016
1681
We conclude by showing that even fair elections can produce unexpected results.
Consider a political party convention at which five different voting schemes are adopted. Assume that there are 110 delegates to this national convention, at which five of the party members, denoted by A, B, C, D, and E, have been nominated as the party’s presidential candidate. Each delegate must rank all five candidates according to his or her choice. Although there are 5! =: 5 × 4 × 3 × 2×1 = 120 possible rankings, many fewer will appear in practice because electors typically split into blocs with similar rankings. Let’s assume that our 110 delegates submit only six different preference lists, as indicated in the following preference profile:
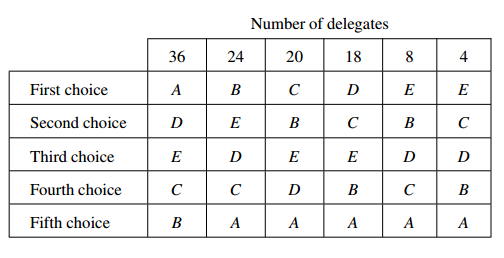
The 36 delegates who most favor nominee A rank D second, E third, C fourth, and B fifth. Although A has the most first-place votes, he is actually ranked last by the other 74 delegates. The 12 electors who most favor nominee E split into two subgroups of 8 and 4 because they differ between B andC on their second and fourth rankings.
We shall assume that our delegates must stick to these preference schedules throughout the following five voting agendas. That is, we will not allow any delegate to switch preference ordering in order to vote in a more strategic manner or because of new campaigning.
We report the results when six popular voting methods are used. There are six different results.
1. Majority. As one might expect with five candidates, there is no majority winner.
2. Plurality. If the party were to elect its candidate by a simple plurality, nominee A would win with 36 first-place votes, in spite of the fact that A was favored by less than one-third of the electorate and was ranked dead last by the other 74 delegates.
3. Runoff. On the other hand, if the party decided that a runoff election should be held between the top two contenders (A and B), who together received a majority of the first-place votes in the initial plurality ballot, then candidate B outranks A on 74 of the 110 preference schedules and is declared the winner in the runoff.
4. Hare Method. Suppose the Hare method is used: a sequence of ballots is held, and eliminating at each stage the nominee with the fewest first-place votes. The last to survive this process becomes the winning candidate. In our example E, with only 12 first-place votes, is eliminated in the first round. E can then be deleted from the preference profile, and all 110 delegates will vote again on successive votes. On the second ballot, the 12 delegates who most favored E earlier now vote for their second choices, that is, 8 for B and 4 for C; the number of first-place votes for the four remaining nominees is

Thus, D is eliminated. On the third ballot the 18 first-place votes for D are reassigned to C, their second choice, giving

Now B is eliminated. On the final round, 74 of the 110 delegates favor C over A, and therefore C wins.
5. Borda Count. Given that they have the complete preference schedule for each delegate, the party might choose to use a straight Borda count to pick the winner.
They assign five points to each first-place vote, four points for each second, three points for a third, two points for a fourth, and one point for a fifth. The scores are:
A: 254 = (5)(36)+(4)(0)+(3)(0)+(2)(0)+(1)(24+20+18+8+4)
B: 312 = (5)(24)+(4)(20+8)+(3)(0)+(2)(18+4)+(1)(36)
C: 324 = (5)(20)+(4)(18+4)+(3)(0)+(2)(36+24+8)+(1)(0)
D: 382 = (5)(18)+(4)(36)+(3)(24+8+4)+(2)(20)+(1)(0)
E: 378 = (5)(8+4)+(4)(24)+(3)(36+20+18)+(2)(0)+(1)(0)
The highest total score of 382 is achieved by D, who then wins. A has the lowest score (254) and B the second lowest (312).
6. Condorcet. With five candidates, there is often no Condorcet winner. However, when we make the head-to-head comparisons, we see that E wins out over:
• A by a vote of 74 to 36
• B by a vote of 66 to 44
• C by a vote of 72 to 38
• D by a vote of 56 to 54
So there is a Condorcet winner, namely E.
In summary, our political party has employed five different common voting procedures and has come up with five different winning candidates. We see from this illustration that those with the power to select the voting method may well determine the outcome, simply by choosing the voting method.
 الاكثر قراءة في الرياضيات التطبيقية
الاكثر قراءة في الرياضيات التطبيقية
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















