Kennedy and Levin (2002)

In presenting Kennedy and Levin’s account,¹ I make use of a four-sorted type-logical language, with sorts for ordinary individuals (x, x), events (e, e), times (t, t), and degrees (d, d). Degrees for Kennedy and Levin are positive or negative intervals on a scale, where a scale is modeled as the set of real numbers between 0 and 1. More precisely, a scale S may be closed, open, closed at 0 (and open at 1), or closed at 1 (and open at 0):

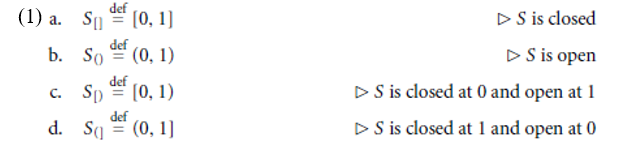
Kennedy and Levin speak explicitly only of closed and open scales, that is, of the cases in (10a) and (10b). However, it seems that half-closed scales play a more important role in their analyses than open scales (e.g., the scale of length is closed at 0 and open at 1). Indeed, it is unclear whether open scales or scales closed at 1 and open at 0 are ever really needed in their framework. Accordingly, I will restrict my attention to closed scales and scales closed at 0 and open at 1 in the following discussion.

Positive and negative degrees for closed scales and scales closed at 0 and open at 1 are defined as follows, where p is a chosen point on the scale in question:

According to the definition in (11a), the minimal positive degree is [0, 0] (i.e., 0) if S is closed or closed at 0 and open at 1, the maximal positive degree is [0, 1] if S is closed, and there is no maximal positive degree if S is closed at 0 and open at 1, because S does not include 1 in this case. In contrast, the definition in (11b) states that the minimal negative degree is [1, 1] (i.e., 1) if S is closed, but there is no minimal negative degree if S is closed at 0 and open at 1. Finally, the maximal negative degree is [0, 1] if S is closed, but there is no maximal negative degree if S is closed at 0 and open at 1. Observe that negative degrees have nothing to do with negative numbers – the essential difference between positive and negative degrees depends on whether the degrees (as intervals) begin at the bottom of the scale and go upwards (positive degrees) or begin at the end of the scale and go downwards (negative degrees).

As long as S is closed or closed at 0 and open at 1, positive degrees are closed at the right and negative degrees are closed at the left by definition. Accordingly, we can say that the maximal point of a positive degree is its rightmost point, whereas the maximal point of a negative degree is its leftmost point:

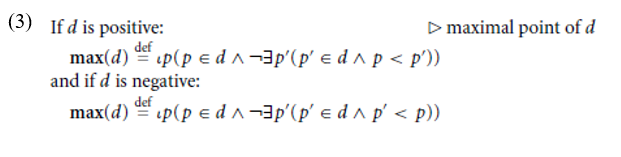
As Kennedy and Levin point out, this model of degrees allows for the ‘addition’ (+       ) of degrees to be expressed. In the case of two positive degrees, the idea is that the lengths of the two degrees are added together to yield a greater positive degree. Note that + in (13) stands for arithmetic addition.²

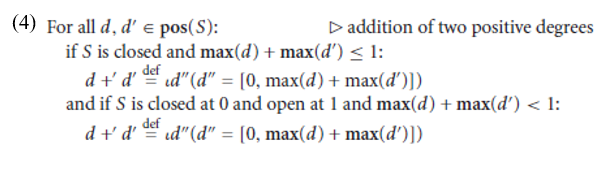
For example, if S is closed at 0 and open at 1, d is [0, .4], and d   is [0, .2], then d +  d         is [0, .6], given that .6 = .4 + .2 and the condition that .6 is less than 1 is fulfilled.

The addition of a negative degree and a positive degree is less straightforward. However, the intuitive strategy is to increase the length of the negative degree by the length of the positive degree to arrive at a potentially greater negative degree. Formally, this amounts to subtracting the maximal point of the positive degree from the maximal point of the negative degree:³

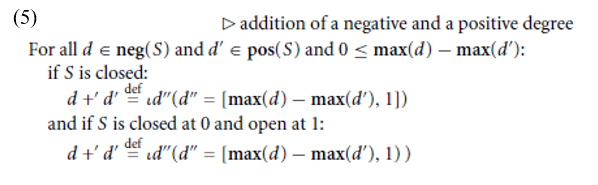
As an illustration, if S is closed, d is [.5, 1] (a negative degree), and d    is [0, .3] (a positive degree), then d +    d         is [.2, 1], because .2 = .5 − .3 and the condition that 0 is less than or equal to .2 is satisfied.⁴

An attractive feature of Kennedy and Levin’s approach is that it offers an insightful analysis of pairs of gradable adjectives such as long/short. Kennedy and Levin take such adjectives to denote functions from individuals and times to degrees. For example, long is analyzed as the function long, where long(x)(t) is read as “the degree to which individual x is long at time t”. To get things off the ground, it also needs to be postulated both that the scale of length is closed at 0 and open at 1 and that degrees of length are positive:

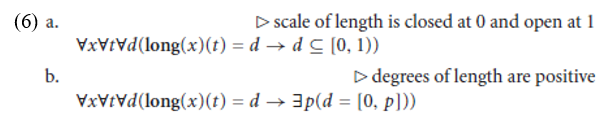
The meaning of short can then be defined in terms of the meaning of long: the degree to which x is short at t is identical to the negative degree d whose maximal point is equal to the maximal point of the (positive) degree d        to which x is long at t, as formalized in (7).

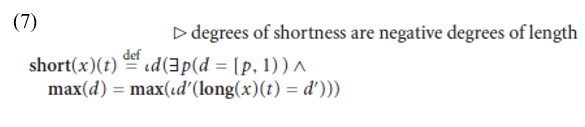
For instance, suppose that the (positive) degree to which x is long at t is [0, .4]. Then, according to this definition, the (negative) degree to which x is short at t is [.4, 1), because the maximal point of [0, .4] is .4. In general, a hallmark of Kennedy and Levin’s approach is to model what appear to be lesser degrees (e.g., “x is shorter than y (at t)”) and decreases in degrees (e.g.,“x is shortened”) with respect to some property (e.g., length) as in fact greater negative degrees and increases in negative degrees, respectively, with respect to that property.

1 My presentation is largely based on Kennedy and Levin (2002), which has its roots in Hay et al. (1999), Kennedy and McNally (1999), and Kennedy (2001). Note that I do not always recite Kennedy and Levin’s formulations verbatim and often take the liberty of reformulating certain points. Kennedy and Levin (this volume) update their account of degree achievements. Although, for reasons of timing, I do not discuss their updated account here, I believe that the essence of my evaluation largely applies to their updated account as well, given that my points concern more the adequacy of their analysis as an approach to aspectual composition and less the details of how to treat degree achievements per se.

2 This definition differs from Kennedy and Levin’s in that it makes explicit the condition that the sum of the two maximal points should not be greater than 1 if S is closed and less than 1 if S is closed at 0 and open at 1, for otherwise the maximal point of the resulting degree would fall “off the scale,” so to speak, which should be avoided. This at once brings out an intuitive difficulty with the formal notion of degree addition appealed to by Kennedy and Levin, namely, that it is neither as general nor as innocent as it initially appears.

3 This definition differs in two respects from Kennedy and Levin’s. Firstly, and less importantly, it has two subcases, depending on whether S is closed or closed at 0 and open at 1, whereas Kennedy and Levin’s assumes that S is closed (and the definition in Hay et al. 1999 assumes that S is closed at 0 and open at 1). Secondly, and more importantly, it makes explicit the condition that the difference of the maximal point of the negative degree and the maximal point of the positive degree should be at least 0, for if it were not, the maximal point of the resulting negative degree would also fall “off the scale,” though this time to the left, similarly to be avoided. Again, this reaffirms the intuitive difficulty mentioned in note 11.

4 Hay et al. (1999) claim that the addition of two negative degrees is undefined. Although this may be desirable for empirical reasons, the technical apparatus would certainly allow for the addition of two negative degrees to be defined, even if it would have to be restricted in a way similar to how the addition of other degrees has to be (see notes 11 and 12). For example, one could imagine defining the addition of two negative degrees d and d in terms of the addition of their respective maximal points, analogously to the addition of two positive degrees. In this case, the addition of two negative degrees would generally result in a lesser negative degree.