
تاريخ الفيزياء

علماء الفيزياء


الفيزياء الكلاسيكية

الميكانيك

الديناميكا الحرارية


الكهربائية والمغناطيسية

الكهربائية

المغناطيسية

الكهرومغناطيسية


علم البصريات

تاريخ علم البصريات

الضوء

مواضيع عامة في علم البصريات

الصوت


الفيزياء الحديثة


النظرية النسبية

النظرية النسبية الخاصة

النظرية النسبية العامة

مواضيع عامة في النظرية النسبية

ميكانيكا الكم

الفيزياء الذرية

الفيزياء الجزيئية


الفيزياء النووية

مواضيع عامة في الفيزياء النووية

النشاط الاشعاعي


فيزياء الحالة الصلبة

الموصلات

أشباه الموصلات

العوازل

مواضيع عامة في الفيزياء الصلبة

فيزياء الجوامد


الليزر

أنواع الليزر

بعض تطبيقات الليزر

مواضيع عامة في الليزر


علم الفلك

تاريخ وعلماء علم الفلك

الثقوب السوداء


المجموعة الشمسية

الشمس

كوكب عطارد

كوكب الزهرة

كوكب الأرض

كوكب المريخ

كوكب المشتري

كوكب زحل

كوكب أورانوس

كوكب نبتون

كوكب بلوتو

القمر

كواكب ومواضيع اخرى

مواضيع عامة في علم الفلك

النجوم

البلازما

الألكترونيات

خواص المادة


الطاقة البديلة

الطاقة الشمسية

مواضيع عامة في الطاقة البديلة

المد والجزر

فيزياء الجسيمات


الفيزياء والعلوم الأخرى

الفيزياء الكيميائية

الفيزياء الرياضية

الفيزياء الحيوية

الفيزياء العامة


مواضيع عامة في الفيزياء

تجارب فيزيائية

مصطلحات وتعاريف فيزيائية

وحدات القياس الفيزيائية

طرائف الفيزياء

مواضيع اخرى
How a ratchet works
المؤلف:
Richard Feynman, Robert Leighton and Matthew Sands
المصدر:
The Feynman Lectures on Physics
الجزء والصفحة:
Volume I, Chapter 46
2024-06-09
1873
The ratchet is a very simple device which allows a shaft to turn only one way. The possibility of having something turn only one way requires some detailed and careful analysis, and there are some very interesting consequences.
The plan of the discussion came about in attempting to devise an elementary explanation, from the molecular or kinetic point of view, for the fact that there is a maximum amount of work which can be extracted from a heat engine. Of course we have seen the essence of Carnot’s argument, but it would be nice to find an explanation which is elementary in the sense that we can see what is happening physically. Now, there are complicated mathematical demonstrations which follow from Newton’s laws to demonstrate that we can get only a certain amount of work out when heat flows from one place to another, but there is great difficulty in converting this into an elementary demonstration. In short, we do not understand it, although we can follow the mathematics.
In Carnot’s argument, the fact that more than a certain amount of work cannot be extracted in going from one temperature to another is deduced from another axiom, which is that if everything is at the same temperature, heat cannot be converted to work by means of a cyclic process. First, let us back up and try to see, in at least one elementary example, why this simpler statement is true.
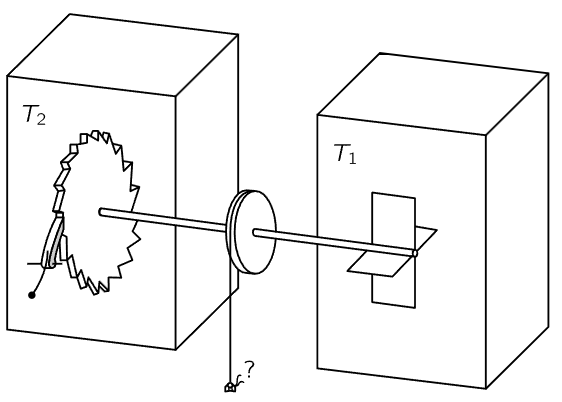
Fig. 46–1. The ratchet and pawl machine.
Let us try to invent a device which will violate the Second Law of Thermodynamics, that is, a gadget which will generate work from a heat reservoir with everything at the same temperature. Let us say we have a box of gas at a certain temperature, and inside there is an axle with vanes in it. (See Fig. 46–1 but take T1= T2= T, say.) Because of the bombardments of gas molecules on the vane, the vane oscillates and jiggles. All we have to do is to hook onto the other end of the axle a wheel which can turn only one way—the ratchet and pawl. Then when the shaft tries to jiggle one way, it will not turn, and when it jiggles the other, it will turn. Then the wheel will slowly turn, and perhaps we might even tie a flea onto a string hanging from a drum on the shaft, and lift the flea! Now let us ask if this is possible. According to Carnot’s hypothesis, it is impossible. But if we just look at it, we see, prima facie, that it seems quite possible. So we must look more closely. Indeed, if we look at the ratchet and pawl, we see a number of complications.
First, our idealized ratchet is as simple as possible, but even so, there is a pawl, and there must be a spring in the pawl. The pawl must return after coming off a tooth, so the spring is necessary.
Another feature of this ratchet and pawl, not shown in the figure, is quite essential. Suppose the device were made of perfectly elastic parts. After the pawl is lifted off the end of the tooth and is pushed back by the spring, it will bounce against the wheel and continue to bounce. Then, when another fluctuation came, the wheel could turn the other way, because the tooth could get underneath during the moment when the pawl was up! Therefore, an essential part of the irreversibility of our wheel is a damping or deadening mechanism which stops the bouncing. When the damping happens, of course, the energy that was in the pawl goes into the wheel and shows up as heat. So, as it turns, the wheel will get hotter and hotter. To make the thing simpler, we can put a gas around the wheel to take up some of the heat. Anyway, let us say the gas keeps rising in temperature, along with the wheel. Will it go on forever? No! The pawl and wheel, both at some temperature T, also have Brownian motion. This motion is such that, every once in a while, by accident, the pawl lifts itself up and over a tooth just at the moment when the Brownian motion on the vanes is trying to turn the axle backwards. And as things get hotter, this happens more often.
So, this is the reason this device does not work in perpetual motion. When the vanes get kicked, sometimes the pawl lifts up and goes over the end. But sometimes, when it tries to turn the other way, the pawl has already lifted due to the fluctuations of the motions on the wheel side, and the wheel goes back the other way! The net result is nothing. It is not hard to demonstrate that when the temperature on both sides is equal, there will be no net average motion of the wheel. Of course the wheel will do a lot of jiggling this way and that way, but it will not do what we would like, which is to turn just one way.
Let us look at the reason. It is necessary to do work against the spring in order to lift the pawl to the top of a tooth. Let us call this energy ϵ, and let θ be the angle between the teeth. The chance that the system can accumulate enough energy, ϵ, to get the pawl over the top of the tooth, is e−ϵ/kT. But the probability that the pawl will accidentally be up is also e−ϵ/kT. So the number of times that the pawl is up and the wheel can turn backwards freely is equal to the number of times that we have enough energy to turn it forward when the pawl is down. We thus get a “balance,” and the wheel will not go around.
 الاكثر قراءة في الميكانيك
الاكثر قراءة في الميكانيك
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















