The substances have different refractive index for light polarized in different directions. Of very practical value are those crystals and other substances in which not only the index, but also the coefficient of absorption, is different for light polarized in different directions. By the same arguments which supported the idea of birefringence, it is understandable that absorption can vary with the direction in which the charges are forced to vibrate in an anisotropic substance. Tourmaline is an old, famous example and polaroid is another. Polaroid consists of a thin layer of small crystals of herapathite (a salt of iodine and quinine), all aligned with their axes parallel. These crystals absorb light when the oscillations are in one direction, and they do not absorb appreciably when the oscillations are in the other direction.

Suppose that we send light into a polaroid sheet polarized linearly at an angle θ to the passing direction. What intensity will come through? This incident light can be resolved into a component perpendicular to the pass direction which is proportional to sin θ, and a component along the pass direction which is proportional to cos θ. The amplitude which comes out of the polaroid is only the cosine θ part; the sin θ component is absorbed. The amplitude which passes through the polaroid is smaller than the amplitude which entered, by a factor cos θ. The energy which passes through the polaroid, i.e., the intensity of the light, is proportional to the square of cos θ. Cos²θ, then, is the intensity transmitted when the light enters polarized at an angle θ to the pass direction. The absorbed intensity, of course, is sin²θ.

An interesting paradox is presented by the following situation. We know that it is not possible to send a beam of light through two polaroid sheets with their axes crossed at right angles. But if we place a third polaroid sheet between the first two, with its pass axis at 45^∘ to the crossed axes, some light is transmitted. We know that polaroid absorbs light, it does not create anything. Nevertheless, the addition of a third polaroid at 45^∘ allows more light to get through.

One of the most interesting examples of polarization is not in complicated crystals or difficult substances, but in one of the simplest and most familiar of situations—the reflection of light from a surface. Believe it or not, when light is reflected from a glass surface it may be polarized, and the physical explanation of this is very simple. It was discovered empirically by Brewster that light reflected from a surface is completely polarized if the reflected beam and the beam refracted into the material form a right angle. The situation is illustrated in Fig. 33–4. If the incident beam is polarized in the plane of incidence, there will be no reflection at all. Only if the incident beam is polarized normal to the plane of incidence will it be reflected. The reason is very easy to understand. In the reflecting material the light is polarized transversely, and we know that it is the motion of the charges in the material which generates the emergent beam, which we call the reflected beam. The source of this so-called reflected light is not simply that the incident beam is reflected; our deeper understanding of this phenomenon tells us that the incident beam drives an oscillation of the charges in the material, which in turn generates the reflected beam. From Fig. 33–4 it is clear that only oscillations normal to the paper can radiate in the direction of reflection, and consequently the reflected beam will be polarized normal to the plane of incidence. If the incident beam is polarized in the plane of incidence, there will be no reflected light.

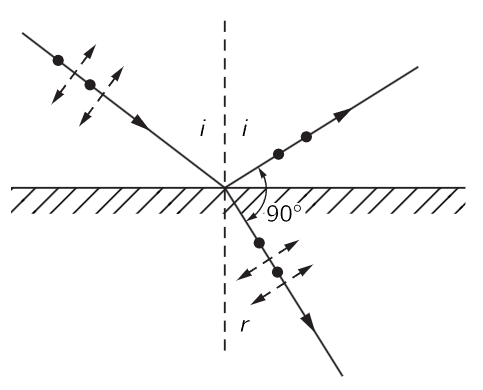
Fig. 33–4. Reflection of linearly polarized light at Brewster’s angle. The polarization direction is indicated by dashed arrows; round dots indicate polarization normal to the paper.

This phenomenon is readily demonstrated by reflecting a linearly polarized beam from a flat piece of glass. If the glass is turned to present different angles of incidence to the polarized beam, sharp attenuation of the reflected intensity is observed when the angle of incidence passes through Brewster’s angle. This attenuation is observed only if the plane of polarization lies in the plane of incidence. If the plane of polarization is normal to the plane of incidence, the usual reflected intensity is observed at all angles.