
خريطة كارنوف: K-MAP) Karnaugh Map)
 المؤلف:
جهاد دريد / عثمان إرفاعية / باسل عبد الحق / يوسف شقير / إبراهيم محمود
المؤلف:
جهاد دريد / عثمان إرفاعية / باسل عبد الحق / يوسف شقير / إبراهيم محمود
 المصدر:
الالكترونيات الصناعية
المصدر:
الالكترونيات الصناعية
 الجزء والصفحة:
ص68–70
الجزء والصفحة:
ص68–70
 2023-08-16
2023-08-16
 9231
9231
يتم استخدام K-MAP بالاعتماد على العلاقة AB + AB̅ = A لتبسيط الاقترانات البولية وبالتالي تبسيط الدارة الرقمية. وتعدّ طريقة K-MAP طريقة فعالة لتبسيط الاقترانات لحد 6 متغيرات. وإذا كان عدد المتغيرات أكبر من ستة يتم استخدم طريقة Quine-Mckluskey)).
تستخدم خريطة K-map مستطيلات تقسم في أعمدة وصفوف بحيث أن أي حد ضرب (Product term) يمكن الحصول عليه من تقاطع صف وعمود. يتم رسم كل صف وعمود بكل حد من الاقتران والمتمم لهذا الحد.
ويتم الرسم بطريقة بحيث أن أي حركة أفقية أو عمودية تغير حالة متغير واحد فقط.
ولاستخدام K-map في تبسيط الاقترانات يتم عمل ما يلي:
- نرسم خريطة مربعات، بحيث يكون هناك مربع لكل حد ضرب (Product term).
- لكل حد ضرب (Product term) في التعبير المطلوب تبسيطه نضع علامة 1 في المربع الذي يمثله.
- نرسم حلقة حول الحدود المتجاورة والحلقة تكون إما أفقية أو عمودية فقط. يتم استخدام المربع نرسم في أكثر من حلقة.
- لكل حلقة لا تكتب الحد المكرر إلا مرة واحدة.
- إذا ظهر الحد ومتممه أخرج من التعبير.
- نكتب التعبير للحدود المتبقية.
- نكتب مجموع الحدود في البند 5، يكون ذلك هو الاقتران المبسط. ويكون الشكل العام لخريطة كارنوف لمتغيرين كما في الشكل التالي.
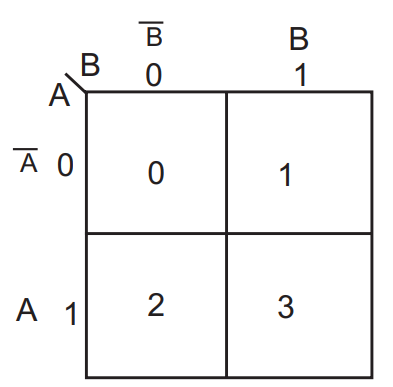
______________________________________________
مثال:
K-map لمتغيرين: لنبدأ بالتعبير AB + AB̅ وهو من متغيرين نرسم مربعاً ونقسمه إلى عمود وصف لكل متغير وقيمته. نضع 1 في كل مربع يمثل حداً من حدود الاقتران الحد الأول هو AB، ولذلك نضع 1 في المربع الأسفل من اليمين.
والحد الثاني AB̅ لذلك نضع 1 في المربع الأسفل من اليسار. نرسم حلقة حول الحدين المتجاورين.
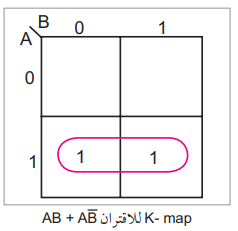
لاحظ أن الحلقة تحتوي على الحدود B̅, A, B, A ولذلك نحذف A واحدة، وكذلك B̅ + B يساوي صفراً، ويتبقى فقط A. إذن تم تبسيط التعبير AB + AB̅ إلى A.
______________________________________________
مثال:
لنأخذ الاقتران:
A̅ B̅ + A B̅+ A̅ B
ونريد أن نكتبه بأبسط صورة.
الحل:
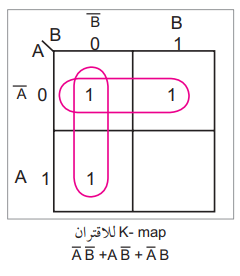
بما أنه يتكون فقط من متغيرين، فإننا نرسم المربعات كما يلي (كما في المثال السابق). ونقوم بالخطوات التالية:
1- نضع 1 في المربع الذي يمثل الحد A B̅
2- نضع 1 في المربع الذي يمثل الحد A̅ B
3- نضع 1 في المربع الذي يمثل الحد A̅ B̅
4- نرسم حلقات حول المربعات المتجاورة.
بسبب وجود حلقتين، فإنه سيكون هناك حدان في الاقتران المبسط. تحتوي الحلقة العمودية على الحدود A̅ B̅, A̅ B ولذلك نحذف المتغير المكرر.
وكذلك B+ 1 = B̅، إذاً يتبقى الحد A̅.
تحتوي الحلقة الأفقية على الحدود
A̅ B̅ ,A B̅
ولذلك يتبقى فقط الحد B̅.
إذن تصبح النتيجة A̅ + B̅. ومنها تستنتج أن
A B̅ + A̅ B+ A̅ B̅ = A̅ + B̅
______________________________________________
مثال:
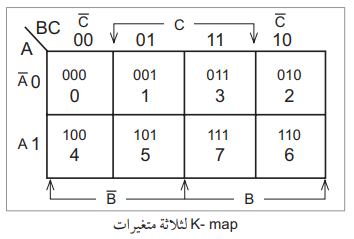
K-map: لثلاثة متغيرات:
يبين الشكل التالي MAP-K لثلاثة متغيرات.
وكما في حالة المتغيرين، فإن المربعات المتجاورة تختلف فقط في حالة تغير واحد. تعدّ الأطراف (يميناً ويساراً) وأعلى وأسفل متجاورة كما لو أنها ملفوفة على أسطوانة.
______________________________________________
مثال:
يوضح الجدول التالي جدول الصواب لأحد الاقترانات البولية المطلوب هو أن نجد الاقتران ونمثله بالدارات المنطقية. بعد ذلك نستخدم K-map لتبسيط الاقتران ونمثله بالدارات المنطقية.
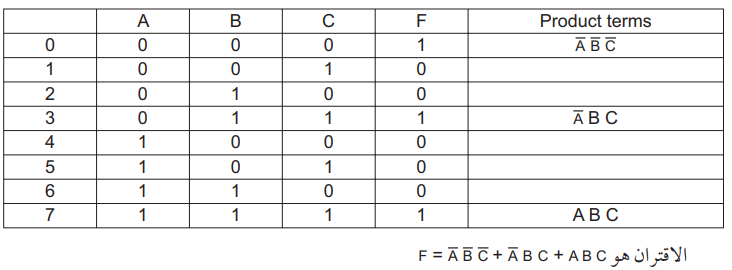
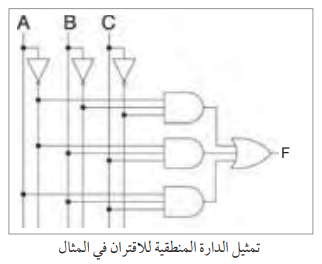
وتكون الداراة المنطقية التي تمثله كما في الشكل التالي: لاحظ أن الجدول أنتج اقتراناً بثلاثة حدود.
تقاس عادة درجة تعقيد الدارة بعدد مداخل البوابات. لاحظ أن الدارة السابقة تحتوي على 15 مدخلاً (11 بوابة). والآن نستخدم K-Map لتبسيط الاقتران كما في الشكل
التالي:
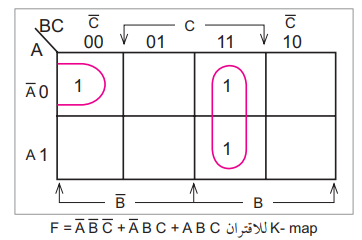
لاحظ أن الحلقة تحيط بالحدود
ABC,A̅BC
وهما الحدان المتجاوران على ظهر الأسطوانة. وبما أن A إذن يتبقى BC فقط.
يمثل الحد A̅ B̅ C̅ مربعاً بحد ذاته. إذن يصبح الاقتران
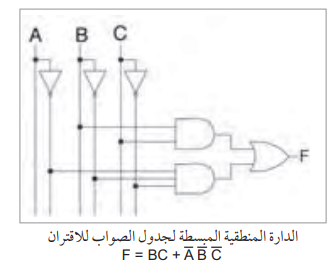
F = BC + A̅ B̅ C̅
والدارة المناظرة له كما في الشكل التالي:
لاحظ أن عدد المداخل، هذه الدارة أصبح عشرة بدلاً من 15 كما كان في التمثيل السابق (عدد البوابات 6).
 الاكثر قراءة في الألكترونيات
الاكثر قراءة في الألكترونيات
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


