إلى الآن اقتصر تركيزي على الاكتشافات الكونية، إلا أن علم الكونيات لن يُعد علما بحق إذا افتقر إلى إطار عمل من النظريات الفيزيائية التي يمكن فهم هذه الاكتشافات داخله. وضع الأساس النظري لعلم الكونيات الحديث منذ حوالي القرن على يد أينشتاين في صورة نظرية النسبية العامة. نُشرت هذه النظرية عام 1915، في الأيام السوداء للحرب العالمية الأولى، إلا أن هذا لم يمنع علماء الفلك والفيزياء من جانبي الصراع من الاهتمام الكبير بما تقوله هذه النظرية عن علم الكونيات. صُممت نظرية النسبية العامة، أو النسبية العامة كما يشار إليها اختصارًا، كي تحل محل نظرية نيوتن للجاذبية الموضوعة في القرن السابع عشر. في علم الكونيات تعد الجاذبية هي القوة المهيمنة، المسيطرة على جميع القوى الأخرى في شتى أرجاء الكون لهذا احتاج علماء الكونيات لنظرية متعلقة بالجاذبية كي يفهموا الكون المتمدد.

تجسدت عبقرية أينشتاين في إدراكه أنه رغم أن الجاذبية تعبر عن نفسها في صورة قوة، فإنه من الممكن فهمها فهما مختلفًا تمامًا، في ضوء ما يعرف بـ «الهندسة المنحنية». دعني أشرح لك ما يعنيه هذا إن قواعد الهندسة التي نتعلمها في المدارس يعود ماضيها إلى وقت الإغريق القدماء، وهي تعرف باسم الهندسة الإقليدية على اسم إقليدس الذي دوّن قواعدها. هناك العديد من القواعد الرياضية التي يمكن إثباتها بالبديهيات الإقليدية، مثال على ذلك قاعدة فيثاغورث الشهيرة من النظريات الأخرى الشهيرة تلك التي تنص على أن مجموع الزوايا الداخلية للمثلث تساوي مجموع زاويتين قائمتين (أي 180 درجة).

إن خصائص الخطوط والدوائر والمثلثات وغيرها من الأشكال لا تحتمل غير تفسير واحد، إلا أن هناك شرطا أساسيا لذلك: وهي أنها تنطبق فقط على الأسطح المستوية. إن هذه النظريات تعمل بمثالية على سبورات الدراسة وألواح الورق الموجود على المكاتب الدراسية، إلا أنها لا تصلح في الأسطح المنحنية أو المطوية كالكرات. يدرك الطيارون والملاحون هذه الحقيقة بشكل تام، وهم يستخدمون قواعد هندسية مختلفة للتأقلم مع تقوس سطح الأرض. على سبيل المثال، على سطح كوكب الأرض يمكن أن يملك المثلث ثلاث زوايا قائمة (انظر الشكل 2-6).

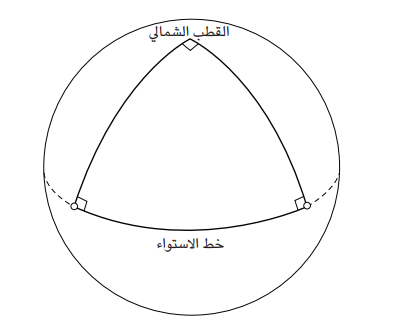
شكل 2-6: الفضاء المنحني. تختلف قواعد الهندسة على السطح الكروي عن تلك الخاصة بالسطح المستوي. على سبيل المثال، قد يحتوي المثلث على ثلاث زوايا قائمة، مثل هذا المثلث المرسوم على سطح الأرض، الذي يصل رأسه إلى القطب الشمالي وتسير قاعدته على امتداد خط الاستواء. السطح الكروي ثنائي الأبعاد الممثل هنا هو نظير للفضاء المنحني ثلاثي الأبعاد.

إذا كان بإمكان الأسطح ثنائية الأبعاد أن تكون إما مستوية (الهندسة الإقليدية) أو منحنية (الهندسة اللاإقليدية)، فهل يمكن أن يكون الفضاء ثلاثي الأبعاد، إما ذا هندسة «مستوية» (إقليدية) أو هندسة منحنية؟ قبل أينشتاين كان الجميع يفترضون أن الفضاء له هندسة «مستوية» أو إقليدية، وأنه يتبع القواعد التي تعلمناها في المدارس للأبعاد الثنائية بشكل تام. إلا أنه لا يوجد سبب منطقي يحتم ذلك. تسلى بعض علماء الرياضيات في القرن التاسع عشر بفكرة أن هندسة الفضاء ثلاثي الأبعاد يمكن أن تكون تعميما لهندسة الأسطح المنحنية. وقد توصلوا للقواعد الهندسية الخاصة بهذا «الفضاء المنحني»، إلا أنه في ذلك الوقت كان ينظر لهذا بوصفه تسلية رياضية لا أكثر. إلا أن كل هذا تغير مع حلول نظرية النسبية العامة، التي اقترح أينشتاين من خلالها أن حقل الجاذبية يمكنه التسبب في انحناء الفضاء ثلاثي الأبعاد، وهو ما يحتم علينا استخدام الهندسة اللاإقليدية لوصفه.

ما هو، إذن، الفضاء المنحني؟ من طرق تخيله: التفكير في مثلث مرسوم حول الشمس (انظر الشكل 2-7). لكن من المهم أن يكون هذا المثلث مستويا (أي يقع على سطح مستو). والآن قس زوايا المثلث واجمعها معا. إذا طبقنا الهندسة الإقليدية على هذا الموقف ستكون النتيجة 180 درجة، لكن أينشتاين زعم أن الإجابة ينبغي أن تكون أكبر قليلًا من 180 درجة، رغم استواء المثلث، وذلك لأن مجال جاذبية الشمس يحني الهندسة ثلاثية الأبعاد للفضاء المحيط به. يمكن إجراء هذه التجربة (بصورة مشابهة) من خلال موجات الرادار المرتدة عن عطارد والزهرة وتثليثها. يتضح لنا أن أينشتاين كان محقا، وأن الفضاء في حقيقة الأمر منحن وليس مسطحًا. (توضيح مهم فيما يخص المصطلحات المستخدمة: حين يتحدث علماء الكونيات عن الفضاء «المسطح» فهم لا يعنون أن الفضاء مسطح مثل الفطيرة، بل يعنون فضاء ثلاثي الأبعاد لكن تنطبق عليه الهندسة الإقليدية.)

أحيانا توصف الهندسة المنحنية بالقرب من الشمس بالقول إن جاذبية الشمس تحني أشعة الضوء المارة بالقرب منها، وفي هذه الحالة سيكون للمثلث زوايا مشوهة بسبب انحراف أضلاعه، وهذا صحيح؛ فهذه طريقة أخرى للتفكير في الفضاء المنحني، مع الوضع في الاعتبار أن الأضلاع المنحرفة هي في حقيقة الأمر أكثر خطوط يمكن رسمها في الهندسة المنحنية استقامة، وعلى هذا لا يقتصر الأمر على مجرد تقويم أشعة الضوء المنحنية ومن ثم استعادة النتائج الإقليدية. إن الفضاء منحن انحناء لا يمكن تقويمه، ولن تفلح أي حيلة في جعله يتوافق مع قواعد الهندسة الإقليدية.

مع أن الفضاء المنحني حول الشمس قابل للقياس فإنه ضئيل للغاية. وقد تأكد وجوده على يد عالم الفلك الإنجليزي أرثر إدينجتون، الذي قاس انحناء الضوء عن طريق ملاحظة الإزاحات الطفيفة في مواضع النجوم في نفس الموضع الذي تحتله الشمس في السماء إبان الكسوف الكلي الذي حدث عام 1919. انحنت أشعة الضوء الصادرة عن النجوم بنفس القدر الذي تنبأت به النسبية العامة، وقد تسبب هذا التأكيد المثير في رفع أينشتاين إلى مكانة المشاهير.

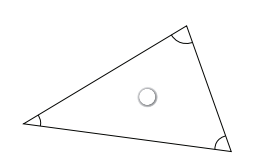
شکل 7-2: الفضاء المنحني حول الشمس. إذا رسمنا مثلثا «مستويا» حول الشمس، يصير مجموع زواياه أكبر بقليل من 180 درجة؛ لأن مجال الجاذبية الشمسي يشوه هندسة الفضاء في الجوار. طريقة أخرى مساوية للتفكير في هذه الظاهرة هي أن نقول إن أضلاع هذا المثلث هي أكثر الخطوط استقامة في الهندسة المنحنية. إذا سلطنا أشعة ضوء على امتداد أضلاع المثلث فسيبدو للمتلقي على الجانب الآخر من الشمس أن الأشعة انثنت قليلًا بفعل جاذبية الشمس.

هوامش

(11) Time is not a dimension of space, but a dimension of spacetime.