Use of Nuclear Magnetic Resonance Spectroscopy in Organic Structural Analysis

The solution of a typical structural analysis problem by nmr methods utilizes at least four kinds of information obtained directly from the spectrum. They are: chemical shifts (δ), line intensities (signal areas), spin-spin splitting patterns (line mulitplicities), and coupling constants (J). We already have shown how chemical shifts are used in the absence of spin-spin splitting. We now will illustrate how more complex spectra may be analyzed.

Figure 9-35 shows the proton nmr spectrum for a compound of formula C3H6O. There are three principal groups of lines at 9.8, 2.4, and 1.0ppm. Look at the multiplicity of these groups before reading further.

Figure 9-35: Nmr spectrum and integral for a compound of formula C3H6O at 60Hz relative to TMS.

There are several ways to approach a problem such as this, but probably the easiest is to start with the integral. The relative heights of the stepped integral for the principal groups of lines can be obtained by a pair of dividers, with a ruler, or with horizontal lines as in Figure 9-35. The integral suggests that one hydrogen is responsible for the resonance at 9.8ppm9.8ppm, two hydrogens at 2.4ppm2.4ppm, and three at 1.0ppm1.0ppm. Three hydrogens in a single group suggest a CH3−CH3− group, and because there is a three-four splitting pattern, it is reasonable to postulate CH3−CH2−. Subtracting C2H5 from the given formula C3H6OC3H6O leaves CHO, which, with normal valences, has to be −CH=O. The spectrum thus appears to be consistent with the structure CH3CH2CH=O (propanal) as judged from the molecular formula and the spin-spin splitting pattern, which indicates the CH3CH2− grouping. To be sure of the structure, we should check it against all of the available information. First, from the shifts (Table 9-4) we see that the single proton at 9.8ppm fits almost perfectly for RCHO, the two-proton −CH2C=O resonance at 2.4ppm is consistent with that reported for −CH2COR, while the three-proton line at 1.0ppm1.0ppm checks with 0.9ppm for CH3R.

What about the couplings? The three-four pattern has a spacing of slightly over 7Hz, which is just right for an ethyl group (compare Figures 9-23 and 9-32). The doubling up (almost obscured by second-order splitting) of the −CH2− resonance and the splitting of the −CH=O resonance into a 1:2:1 triplet indicate about a 2-Hz coupling for the −CH2−CH=O group. Three-bond couplings between −CHO and adjacent −CH2− protons appear to be generally smaller than −CH2−CH3 couplings.

We usually would not rely on nmr alone in a structure-analysis problem of this kind, but would seek clues or corroboration from the infrared, electronic, or other spectra, as well as chemical tests. In later chapters we will have many problems that will be facilitated by the use of both nmr and infrared spectra. A further worked example will illustrate the approach.

A compound has the composition C3H3Br and gives the infrared and nuclear magnetic resonance spectra shown in Figure 9-36. The problem is how to use this information to deduce the structure of the compound. The molecular formula tells us the number and kind of atoms and the number of multiple bonds or rings. The formulas of the corresponding C3 hydrocarbon without the bromine would be C3H4, or four hydrogens less than the saturated alkane C3H8C3H8. This means there must be two double bonds or the equivalent - one triple bond or one ring and one double bond. Because from the formula we suspect unsaturation, we should check this out with the infrared spectrum. There is a band at 2120cm−1, which is indicative of an unsymmetrically substituted −C≡C− group (Table 9-2). The strong, sharp band at 3300cm−1 further tells us that the substance is a 1-alkyne −C≡C−H.

Figure 9-36: Infrared and nmr spectra for a compound of formula C3H3Br. The infrared spectrum here is different from others shown in this book in being linear in wavelength, λ, instead of in wave numbers, ν∼. The units of wavelength here are microns (10−6cm).

The proton nmr spectrum shows that there are only two principal groups of lines - a two-proton doublet at 3.85ppm and a one-proton triplet at 2.45ppm. The two-three splitting pattern combined with the 2:1 proton ratio suggests a CH2 group coupled with a CH group. The structure must be a 3-bromo-propyne, BrCH2C≡CH. To confirm the assignment, the chemical shifts should be checked (Table 9-4). The ≡C−H at 2.45ppm agrees well with the tabulated value of 2.5ppm. There is no tabulated data for −C≡C−CH2Br but the observed shift at 3.85ppm is at slightly lower fields than the tabulated 3.33ppm for −CH2Br. This is expected because of the triple bond. The correlation of Equation 9-4 predicts a value of 4.0ppm.

Very often, a proton will be spin-coupled to two or more different protons, and the couplings are not necessarily the same. When this happens, the resulting spectrum can be quite complex, as our next example shows.

A compound C9H10 gives the nmr spectrum of Figure 9-37. There are clearly four kinds of protons in the molecule at δ=7.28 ppm, 5.35 ppm, 5.11ppm, and 1.81ppm. Although the integral is not shown, the main groups of lines have intensities from the low-field to high-field in the ratio of 5:1:1:3.

Figure 9-37: Nuclear magnetic resonance spectrum of C9H10 at 60MHz. The calibrations are relative to the protons of TMS. The insets show the peaks centered on 321, 307, and 119 Hz with an expanded scale. The spacing between the peaks is 1.5Hz for Group B at 307Hz, and 0.75Hz for Groups A and C at 321 and 119 Hz. The C9H10 protons are coupled to each other, not to A, B, or C.

The five-proton signal at 7.28ppm is typical of a phenyl group, C6H5, and the one-proton signals at 5.35 and 5.11ppm are in the region for alkenic protons, 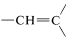. The three-proton signal at 1.81 ppm is typical of a methyl group on a carbon-carbon double bond, .

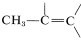There are only three ways to put together a phenyl ring, 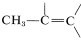, and two HC= protons such that they add up to C9H10. They are

Figure 9-37, and the three mutually coupled groups are labeled as A, B, and C.

Coupling between A and B (designated by the constant JAB) should give four lines, two for A and two for B, as shown in Figure 9-38. Because A and B also are coupled to the three hydrogens of the methyl group (C), each of the four lines corresponding to JAB will be further split (into 1:3:3:1 quartets). If JAC≠JBC, then the spacing of the lines in the two sets of quartets will not be the same.

Figure 9-38: Spin-spin splitting patterns predicted for the nmr signals of the two alkenic protons (A and B) of a methyl-substituted alkene of the type

where JAB≫JB>JAC.

According to the foregoing analysis, the maximum number of lines observable for the A and B resonances is sixteen (8 for A and 8 for B). In fact, only eleven are visible (6 for A and 5 for B), which means that some of the sixteen possible lines must overlap. Without examining all possibilities, we can see that the actual situation can be reproduced if JAB≅JBC=2JAC. The only structure that is consistent with JAB=1.5Hz is 13, or 2-phenylpropene; the other possibilities are excluded because JAB should be about 10Hz for 12 and 16Hz for 11.