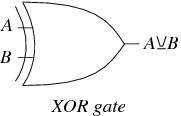
A connective in logic known as the "exclusive or," or exclusive disjunction. It yields true if exactly one (but not both) of two conditions is true. The XOR operation does not have a standard symbol, but is sometimes denoted 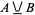 (this work) or  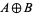(Simpson 1987, pp. 539 and 550-554).  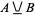is read " 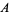aut 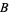," where "aut" is Latin for "or, but not both." The circuit diagram symbol for an XOR gate is illustrated above. In set theory,  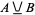is typically called the symmetric difference. The XOR function is implemented as Xor[predicate1, predicate2, ...].

The binary XOR operation 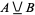 is identical to nonequivalence 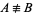.  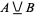can be implemented using AND and OR gates as

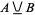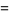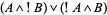			(1)
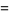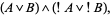			(2)

where 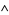 denotes AND and  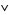denotes OR, and can be implemented using only NOT and NAND gates as

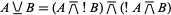(3)

(Simpson 1987), where 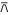 denotes NAND.

The binary XOR operator has the following truth table.

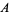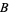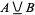T	T	F
T	F	T
F	T	T
F	F	F

The binomial coefficient 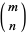 mod 2 can be computed using the XOR operation  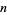XOR 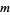, making Pascal's triangle mod 2 very easy to construct.

For multiple arguments, XOR is defined to be true if an odd number of its arguments are true, and false otherwise. This definition is quite common in computer science, where XOR is usually thought of as addition modulo 2. In this context, it arises in polynomial algebra modulo 2, arithmetic circuits with a full adder, and in parity generating or checking. While this means that the multiargument "XOR" can no longer be thought of as "the exclusive OR" operation, this form is rarely used in mathematical logic and so does not cause very much confusion. The XOR operation is associative, so 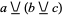 is the same as 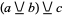. Computation of the multiargument XOR requires evaluation of all its arguments to determine the truth value, and hence there is no "lazy" special evaluation form (as there is for AND and OR).

The ternary XOR operator therefore has the following truth table.

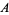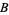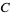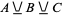T	T	T	T
T	T	F	F
T	F	T	F
T	F	F	T
F	T	T	F
F	T	F	T
F	F	T	T
F	F	F	F

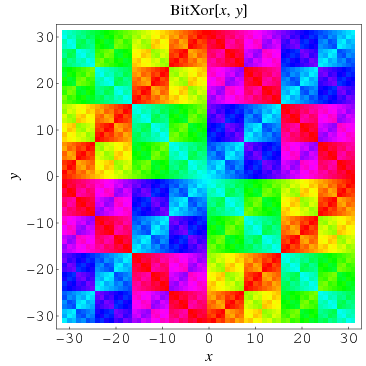
A bitwise version of XOR can also be defined that performs a bitwise XOR on the binary digits of two numbers  and 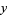 and then converts the resulting binary number back to decimal. Bitwise XOR is implemented in the Wolfram Language as BitXor[n1, n2, ...]. The illustration above plots the bitwise XOR of the array of numbers from  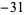to 31 (Stewart 2000; Rangel-Mondragon; Wolfram 2002, p. 871).

REFERENCES:

 Rangel-Mondragon, J. "A Catalog of Cellular Automata." http://library.wolfram.com/infocenter/MathSource/505/.

Simpson, R. E. "The Exclusive OR (XOR) Gate." §12.5.6 in Introductory Electronics for Scientists and Engineers, 2nd ed. Boston, MA: Allyn and Bacon, pp. 550-554, 1987.

Stewart, I. "A Fractal Guide to Tic-Tac-Toe." Sci. Amer. 283, 86-88, 2000.

Wolfram, S. A New Kind of Science. Champaign, IL: Wolfram Media, p. 871, 2002.

اخر الاخبار

اخبار العتبة العباسية المقدسة

العتبة العباسية المقدسة تنظّم مسيرات عزائية لإحياء ذكرى عاشوراء في نينوى

قسم الشؤون الفكرية يحيي ذكرى استشهاد الإمام الحسين (عليه السلام) في القارة الإفريقية

قسمُ التربية والتعليم يقيم مجلسه العزائي السنوي بذكرى عاشوراء

معهد القرآن الكريم النسوي يُقيم مجلس عزاء حسيني إحياءً لذكرى عاشوراء

المزيد

الآخبار الصحية

تناول الجبن.. مفيد للجسم أم خطر يهدد صحتك؟

طبيبة أسنان تحذر.. لا تتجاهل هذه العلامة بعد التنظيف

يجب أن تأكل المزيد من الشمام هذا الصيف.. إليك السبب ؟

تأثير صحي كبير.. كم بيضة يجب أن تتناول يوميا؟

المزيد

الآخبار التكنلوجية

أداء خلايا البيروفسكايت الشمسية تحت الماء قد يزيد كفاءة تحويل الكهرباء

مسافة الأمان: أساس القيادة الآمنة وتجنب الحوادث

هل القيادة السريعة تعني استهلاك اكثر للوقود؟

لماذا يعتبر كوكب المريخ غير صالح للحياة؟

المزيد