0,1-Simple Lattice
المؤلف:
Grätzer, G
المصدر:
General Lattice Theory, 2nd ed. Boston, MA: Birkhäuser, 1998.
الجزء والصفحة:
...
31-12-2021
1608
0,1-Simple Lattice
Let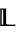 
be a nontrivial bounded lattice (or a nontrivial complemented lattice, etc.). If every nonconstant lattice homomorphism defined on 
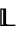is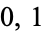 
-separating, then 
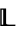is a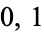 
-simple lattice.
One can show that the following are equivalent for a nontrivial bounded lattice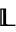 
:
1. The lattice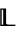 
is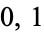 
-simple;
2. There is a largest nontrivial congruence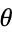 
of 
, and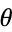 
satisfies both ![[1]_theta=<span style=]()
{1}" src="https://mathworld.wolfram.com/images/equations/01-SimpleLattice/Inline12.gif" style="height:16px; width:51px" /> and ![[0]_theta=<span style=]()
{0}" src="https://mathworld.wolfram.com/images/equations/01-SimpleLattice/Inline13.gif" style="height:16px; width:51px" />.
This result is useful in the study of congruence lattices of finite algebras.
REFERENCES:
Grätzer, G. General Lattice Theory, 2nd ed. Boston, MA: Birkhäuser, 1998.
Hobby, D. and McKenzie, R. The Structure of Finite Algebras. Providence, RI: Amer. Math. Soc., 1988.
Insall, M. "Some Finiteness Conditions in Lattices Using Nonstandard Proof Methods." J. Austral. Math. Soc. 53, 266-280, 1992.
الاكثر قراءة في نظرية المجموعات
اخر الاخبار
اخبار العتبة العباسية المقدسة
