Cardinal Comparison
المؤلف:
Rubin, J. E
المصدر:
Set Theory for the Mathematician. New York: Holden-Day, 1967.
الجزء والصفحة:
...
26-12-2021
1397
Cardinal Comparison
For any sets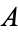 
and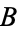 
, their cardinal numbers satisfy 
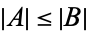iff there is a one-to-one function 
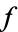from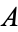 
into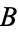 
(Rubin 1967, p. 266; Suppes 1972, pp. 94 and 116). It is easy to show this satisfies the reflexive and transitive axioms of a partial order. However, it is difficult to show the antisymmetry property, whose proof is known as the Schröder-Bernstein theorem. To show the trichotomy property, one must use the axiom of choice.
Although an order type can be defined similarly, it does not seem usual to do so.
REFERENCES:
Rubin, J. E. Set Theory for the Mathematician. New York: Holden-Day, 1967.
Suppes, P. Axiomatic Set Theory. New York: Dover, 1972.
الاكثر قراءة في نظرية المجموعات
اخر الاخبار
اخبار العتبة العباسية المقدسة
