Differential evolution is a stochastic parallel direct search evolution strategy optimization method that is fairly fast and reasonably robust. Differential evolution is implemented in the Wolfram Language as NMinimize[f, vars, Method -> "DifferentialEvolution"] and NMaximize[f, vars, Method -> "DifferentialEvolution"].

Differential evolution is capable of handling nondifferentiable, nonlinear and multimodal objective functions. It has been used to train neural networks having real and constrained integer weights.

In a population of potential solutions within an 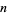-dimensional search space, a fixed number of vectors are randomly initialized, then evolved over time to explore the search space and to locate the minima of the objective function.

At each iteration, called a generation, new vectors are generated by the combination of vectors randomly chosen from the current population (mutation). The outcoming vectors are then mixed with a predetermined target vector. This operation is called recombination and produces the trial vector. Finally, the trial vector is accepted for the next generation if and only if it yields a reduction in the value of the objective function. This last operator is referred to as a selection.

REFERENCES:

Ilonen, J.; Kamarainen, J. K.; and Lampinen, J. "Differential Evolution Training Algorithm for Feed Forward Neural Networks." Neurol. Proc. Lett. 17, 93-105, 2003.

Plagianakos, V. P. and Vrahatis, M. N. "Parallel Evolutionary Training Algorithms for Hardware-Friendly Neural Networks." Natural Comp. 1, 307-322, 2002.

Price, K. and Storn, R. "Differential Evolution." Dr. Dobb's J., Issue 264, 18-24 and 78, Apr. 1997.

Storn, R. "System Design by Constraint Adaptation and Differential Evolution." IEEE Trans. Evol. Comput. 3, 22-34, 1999.

Storn, R. and Price, K. "Differential Evolution: A Simple and Efficient Adaptive Scheme for Global Optimization over Continuous Spaces." J. Global Optimization 11, 341-359, 1997.

اخر الاخبار

اخبار العتبة العباسية المقدسة

بمشاركة الأمين العام للعتبة العبّاسية المقدّسة.. موكب عزاء السادة الخَدَم يحيي ليلة عاشوراء

صحفيّون يشيدون بالتسهيلات الإعلامية التي تقدّمها العتبة العباسية المقدّسة خلال زيارة عاشوراء

أهالي كربلاء ينظّمون مسيرة الشموع الحسينية إحياءً لليلة العاشر من شهر المحرّم

عبر مجلس عزاء.. العتبة العباسية المقدّسة تحيي ليلة اليوم العاشر من المحرّم

المزيد

الآخبار الصحية

لهذا السبب.. إغلاق 25 مركزًا لعلاج الإدمان في مصر ؟

خلافا للاعتقاد الشائع.. علماء يكشفون أسرار بذور البطيخ ؟!

هذا ما يحدث لجسمك عند تناولك الطماطم بانتظام !

تعرف على أطعمة تسرّع "تعافي الجسم" من حروق الشمس

المزيد

الآخبار التكنلوجية

الثلوج تغطي الصحراء الأكثر جفافا في العالم!

بتلسكوب "ألما".. التقاط صورا غير مسبوقة لبدايات الكون !

هل هاتفك مراقب؟.. 5 علامات خطيرة تكشف التجسس عليك

دبي تطلق أول رحلة تجريبية للتاكسي الجوي

المزيد