
Generalized Minimal Residual Method
 المؤلف:
Arnoldi, W
المؤلف:
Arnoldi, W
 المصدر:
"The Principle of Minimized Iterations in the Solution of the Matrix Eigenvalue Problem." Quart. Appl. Math. 9
المصدر:
"The Principle of Minimized Iterations in the Solution of the Matrix Eigenvalue Problem." Quart. Appl. Math. 9
 الجزء والصفحة:
...
الجزء والصفحة:
...
 1-12-2021
1-12-2021
 2106
2106
Generalized Minimal Residual Method
The generalized minimal residual (GMRES) method (Saad and Schultz 1986) is an extension of the minimal residual method (MINRES), which is only applicable to symmetric systems, to unsymmetric systems. Like MINRES, it generates a sequence of orthogonal vectors, but in the absence of symmetry this can no longer be done with short recurrences; instead, all previously computed vectors in the orthogonal sequence have to be retained. For this reason, "restarted" versions of the method are used.
In the conjugate gradient method, the residuals form an orthogonal basis for the space
![span<span style=]() {r^((0)),Ar^((0)),A^2r^((0))}. " src="https://mathworld.wolfram.com/images/equations/GeneralizedMinimalResidualMethod/NumberedEquation1.gif" style="height:21px; width:143px" /> {r^((0)),Ar^((0)),A^2r^((0))}. " src="https://mathworld.wolfram.com/images/equations/GeneralizedMinimalResidualMethod/NumberedEquation1.gif" style="height:21px; width:143px" /> |
In GMRES, this basis is formed explicitly:
The reader may recognize this as a modified Gram-Schmidt orthonormalization. Applied to the Krylov sequence ![<span style=]() {A^kr^((0))}" src="https://mathworld.wolfram.com/images/equations/GeneralizedMinimalResidualMethod/Inline1.gif" style="height:21px; width:46px" /> this orthogonalization is called the "Arnoldi method" (Arnoldi 1951). The inner product coefficients
{A^kr^((0))}" src="https://mathworld.wolfram.com/images/equations/GeneralizedMinimalResidualMethod/Inline1.gif" style="height:21px; width:46px" /> this orthogonalization is called the "Arnoldi method" (Arnoldi 1951). The inner product coefficients 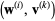 and
and 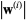 are stored in an upper Hessenberg matrix.
are stored in an upper Hessenberg matrix.
The GMRES iterates are constructed as
where the coefficients 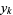 have been chosen to minimize the residual norm
have been chosen to minimize the residual norm 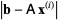 . The GMRES algorithm has the property that this residual norm can be computed without the iterate having been formed. Thus, the expensive action of forming the iterate can be postponed until the residual norm is deemed small enough.
. The GMRES algorithm has the property that this residual norm can be computed without the iterate having been formed. Thus, the expensive action of forming the iterate can be postponed until the residual norm is deemed small enough.
In this scheme, UPDATE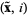 replaces the following computations:
replaces the following computations:
The generalized minimal residual method is designed to solve nonsymmetric linear systems (Saad and Schultz 1986) The most popular form of GMRES is based on a modified Gram-Schmidt orthonormalization procedure and uses restarts to control storage requirements.
If no restarts are used, GMRES (like any orthogonalizing Krylov subspace method) will converge in no more than 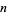 steps (assuming exact arithmetic). Of course this is of no practical value when
steps (assuming exact arithmetic). Of course this is of no practical value when 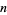 is large; moreover, the storage and computational requirements in the absence of restarts are prohibitive. Indeed, the crucial element for successful application of GMRES(
is large; moreover, the storage and computational requirements in the absence of restarts are prohibitive. Indeed, the crucial element for successful application of GMRES(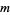 ) revolves around the decision of when to restart; that is, the choice of
) revolves around the decision of when to restart; that is, the choice of 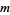 . Unfortunately, there exist examples for which the method stagnates and convergence takes place only at the
. Unfortunately, there exist examples for which the method stagnates and convergence takes place only at the 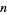 th step. For such systems, any choice of
th step. For such systems, any choice of 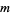 less than
less than 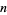 fails to converge.
fails to converge.
Saad and Schultz (1986) have proven several useful results. In particular, they show that if the coefficient matrix 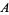 is real and nearly positive definite, then a "reasonable" value for
is real and nearly positive definite, then a "reasonable" value for 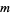 may be selected. Implications of the choice of
may be selected. Implications of the choice of 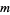 are discussed below.
are discussed below.
A common implementation of GMRES is suggested by Saad and Schultz (1986) and relies on using modified Gram-Schmidt orthonormalization. Householder transformations, which are relatively costly but stable, have also been proposed. The Householder approach results in a three-fold increase in work associated with inner products and vector updates (not with matrix vector products); however, convergence may be better, especially for ill-conditioned systems (Walker 1988). From the point of view of parallelism, Gram-Schmidt orthonormalization may be preferred, giving up some stability for better parallelization properties (Demmel et al. 1993). Here we adopt the modified Gram-Schmidt approach.
The major drawback to GMRES is that the amount of work and storage required per iteration rises linearly with the iteration count. Unless one is fortunate enough to obtain extremely fast convergence, the cost will rapidly become prohibitive. The usual way to overcome this limitation is by restarting the iteration. After a chosen number of iterations 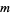 , the accumulated data are cleared and the intermediate results are used as the initial data for the next
, the accumulated data are cleared and the intermediate results are used as the initial data for the next 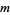 iterations. This procedure is repeated until convergence is achieved. The difficulty is in choosing an appropriate value for
iterations. This procedure is repeated until convergence is achieved. The difficulty is in choosing an appropriate value for 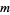 . If
. If 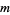 is too small, GMRES(
is too small, GMRES(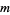 ) may be slow to converge, or fail to converge entirely. A value of
) may be slow to converge, or fail to converge entirely. A value of 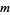 that is larger than necessary involves excessive work (and uses more storage). Unfortunately, there are no definite rules governing the choice of
that is larger than necessary involves excessive work (and uses more storage). Unfortunately, there are no definite rules governing the choice of 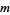 ; choosing when to restart is a matter of experience.
; choosing when to restart is a matter of experience.
For a discussion of GMRES for vector and shared memory computers see Dongarra et al. (1991). For more general architectures, see Demmel et al. (1993).
REFERENCES:
Arnoldi, W. "The Principle of Minimized Iterations in the Solution of the Matrix Eigenvalue Problem." Quart. Appl. Math. 9, 17-29, 1951.
Barrett, R.; Berry, M.; Chan, T. F.; Demmel, J.; Donato, J.; Dongarra, J.; Eijkhout, V.; Pozo, R.; Romine, C.; and van der Vorst, H. Templates for the Solution of Linear Systems: Building Blocks for Iterative Methods, 2nd ed. Philadelphia, PA: SIAM, 1994. http://www.netlib.org/linalg/html_templates/Templates.html.
Demmel, J.; Heath, M.; and van der Vorst, H. "Parallel Numerical Linear Algebra." In Acta Numerica, Vol. 2. Cambridge, England: Cambridge University Press, 1993.
Dongarra, J.; Duff, I.; Sorensen, D.; and van der Vorst, H. Solving Linear Systems on Vector and Shared Memory Computers. Philadelphia, PA: SIAM, 1991.
Saad, Y. and Schultz, M. "GMRES: A Generalized Minimal Residual Algorithm for Solving Nonsymmetric Linear Systems." SIAM J. Sci. Statist. Comput. 7, 856-869, 1986.
Walker, H. F. "Implementation of the GMRES Method using Householder Transformations." SIAM J. Sci. Statist. Comput. 9, 152-163, 1988.
 الاكثر قراءة في الرياضيات التطبيقية
الاكثر قراءة في الرياضيات التطبيقية
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


