Chebyshev Iteration

Chebyshev iteration is a method for solving nonsymmetric problems (Golub and van Loan 1996, §10.1.5; Varga, 1962, Ch. 5). Chebyshev iteration avoids the computation of inner products as is necessary for the other nonstationary methods. For some distributed memory architectures these inner products are a bottleneck with respect to efficiency. The price one pays for avoiding inner products is that the method requires enough knowledge about the spectrum of the coefficient matrix 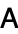 that an ellipse enveloping the spectrum can be identified; this difficulty can be overcome, however, via an adaptive construction developed by Manteuffel (1977) and implemented by Ashby (1985). Chebyshev iteration is suitable for any nonsymmetric linear system for which the enveloping ellipse does not include the origin.

Chebyshev iteration is similar to the conjugate gradient method except that no inner products are computed. Scalars 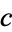 and 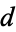 must be selected so that they define a family of ellipses with common center  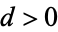and foci  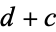and 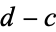 which contain the ellipse that encloses the spectrum (or more generally, the field of values) of  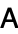and for which the rate  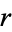of convergence is minimal:

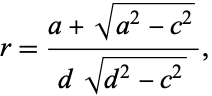where 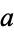 is the length of the 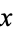-axis of the ellipse.

The pseudocode below assumes that the ellipse degenerates to the interval , i.e., that all eigenvalues are real. For code including the adaptive determination of the iteration parameters 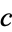 and 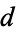, see Ashby (1985).

The Chebyshev method has the advantage over the generalized minimal residual method (GMRES) that only short recurrences are used. On the other hand, GMRES is guaranteed to generate the smallest residual over the current search space. The biconjugate gradient method (BCG), which also uses short recurrences, does not minimize the residual in a suitable norm. However, unlike Chebyshev iteration, they do not require estimation of parameters (the spectrum of 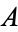). Finally, GMRES and BCG may be more effective in practice, because of superlinear convergence behavior, which cannot be expected for Chebyshev iteration.

For symmetric positive definite systems the ellipse enveloping the spectrum degenerates to the interval  on the positive 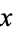-axis, where  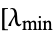and  are the smallest and largest eigenvalues of 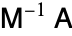, where  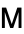is a preconditioner. In circumstances where the computation of inner products is a bottleneck, it may be advantageous to start with the conjugate gradient method, compute estimates of the extremal eigenvalues from the CG coefficients, and then after sufficient convergence of these approximations switch to Chebyshev iteration. A similar strategy may be adopted for a switch from GMRES or BCG methods to Chebyshev iteration.

In the symmetric case (where 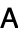 and the preconditioner  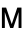are both symmetric), Chebyshev iteration has the same upper bound as the conjugate gradient method provided that  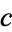and 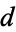 are computed from  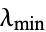and .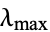

There is a severe penalty for overestimating or underestimating the field of values. For example, if in the symmetric case 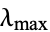 is underestimated, then the method may diverge; if it is overestimated, then the convergence may be very slow. Similar statements can be made for the nonsymmetric case. This implies that one needs fairly accurate bounds on the spectrum of  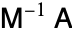for the method to be effective (in comparison with the conjugate gradient method or generalized minimal residual method).

In Chebyshev iteration the iteration parameters are known as soon as one knows the ellipse containing the eigenvalues (or rather, the field of values) of the operator. Therefore the computation of inner products, as is necessary in the generalized minimal residual method and conjugate gradient method, is avoided. This avoids the synchronization points required of conjugate gradient-type methods, so machines with hierarchical or distributed memory may achieve higher performance (it also suggests strong parallelization properties (Saad 1989, Dongarra et al. 1991). Specifically, as soon as one segment of 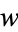 is computed, we may begin computing, in sequence, corresponding segments of 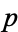, , 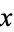and .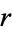

REFERENCES:

Ashby, S. "CHEBYCODE: A Fortran Implementation of Manteuffel's Adaptive Chebyshev Algorithm." Tech. Rep. UIUCDCS-R-85-1203, University of Illinois, 1985.

Barrett, R.; Berry, M.; Chan, T. F.; Demmel, J.; Donato, J.; Dongarra, J.; Eijkhout, V.; Pozo, R.; Romine, C.; and van der Vorst, H. Templates for the Solution of Linear Systems: Building Blocks for Iterative Methods, 2nd ed. Philadelphia, PA: SIAM, 1994. http://www.netlib.org/linalg/html_templates/Templates.html.

Dongarra, J.; Duff, I.; Sorensen, D.; and van der Vorst, H. Solving Linear Systems on Vector and Shared Memory Computers. Philadelphia, PA: SIAM, 1991.

Golub, G. H. and van Loan, C. F. Matrix Computations, 3rd ed. Baltimore, MD: Johns Hopkins, 1996.

Manteuffel, T. "The Tchebychev Iteration for Nonsymmetric Linear Systems." Numer. Math. 28, 307-327, 1977.

Saad, Y. "Krylov Subspace Methods on Supercomputers." SIAM J. Sci. Statist. Comput. 10, 1200-1232, 1989.

Varga, R. Matrix Iterative Analysis. Englewood Cliffs, NJ: Prentice-Hall, 1962.ش