Napier's Bones

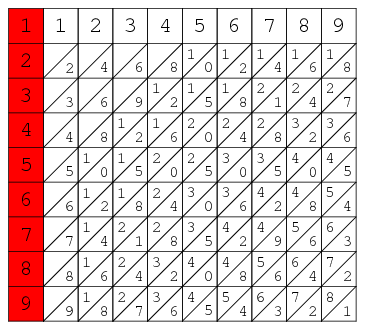
Napier's bones, also called Napier's rods, are numbered rods which can be used to perform multiplication of any number by a number 2-9. By placing "bones" corresponding to the multiplier on the left side and the bones corresponding to the digits of the multiplicand next to it to the right, and product can be read off simply by adding pairs of numbers (with appropriate carries as needed) in the row determined by the multiplier. This process was published by Napier in 1617 an a book titled Rabdologia, so the process is also called rabdology.

There are ten bones corresponding to the digits 0-9, and a special eleventh bone that is used the represent the multiplier. The multiplier bone is simply a list of the digits 1-9 arranged vertically downward. The remainder of the bones each have a digit written in the top square, with the multiplication table for that digits written downward, with the digits split by a diagonal line going from the lower left to the upper right. In practice, multiple sets of bones were needed for multiplication of numbers containing repeated digits.

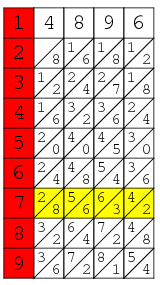
To multiply two numbers, arrange the bones as described above. The above illustration shows this process for 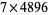. The computation proceeds from right to left, starting with the rightmost bone in the row determined by the multiplier. In this case, the last digit in the 7s row of the 6-bone is 2, so write down 2. Now add the two adjacent numbers in the same row to the left (i.e., the ones in the parallelogram) to obtain 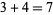, which is the next digit, so we now have 72. The next sum is 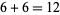, so write down the 2 two obtain 272 and carry the 1. Proceeding to the next digit, it is  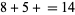(because of the carry), so write down the 4 to obtain  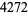and carry the 1. The leftmost digit is then  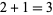(from the carry), giving the final answer .

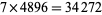While Napier's bones require manual accounting for carries, an ingenious extension known as Genaille rods allows products to simply be read off directly, without the need for carries or even addition of pairs of adjacent digits.

REFERENCES:

Behr, A. "Extracting Square Roots by Means of the Napier Rods." http://www.qnet.fi/abehr/Achim/Calculators_Napier_rods2.html.

Gardner, M. "Napier's Bones." Ch. 7 in Knotted Doughnuts and Other Mathematical Entertainments. New York: W. H. Freeman, pp. 85-93, 1986.

Havil, J. Gamma: Exploring Euler's Constant. Princeton, NJ: Princeton University Press, pp. 17-19, 2003.

Knott, C. G. (Ed.). Napier Tercentenary Memorial Volume. Longmans, 1915.

Leybourn, W. The Art of Numbering by Speaking-Rods: Vulgarly Termed Napier's Bones. London, 1667.

Napier, J. Rabdologia. 1617.

Pappas, T. "Napier's Bones." The Joy of Mathematics. San Carlos, CA: Wide World Publ./Tetra, pp. 64-65, 1989.

Williams, M. R. "From Napier to Lucas: The Use of Napier's Bones in Calculating Instruments." Ann. History of Computing 5, 279-286, 1983.

Williams, M. R. "Napier's Bones." In A History of Computing Technology. Englewood Cliffs, NJ: Prentice-Hall, 1985.