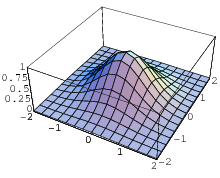Given a function 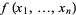 defined on a domain 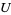, the graph of  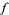is defined as the set of points (which often form a curve or surface) showing the values taken by  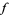over 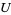 (or some portion of 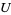). Technically, for real functions,

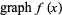		{(x,f(x)) in R^2:x in U}" src="https://mathworld.wolfram.com/images/equations/FunctionGraph/Inline9.gif" style="height:21px; width:134px" />	(1)
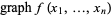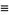		{(x_1,...,x_n,f(x_1,...,x_n)) in R^(n+1):(x_1,...,x_n) in U}." src="https://mathworld.wolfram.com/images/equations/FunctionGraph/Inline12.gif" style="height:21px; width:304px" />	(2)

A graph is sometimes also called a plot. Unfortunately, the word "graph" is uniformly used by mathematicians to mean a collection of vertices and edges connecting them. In some education circles, the term "vertex-edge graph" is used in an attempt to distinguish the two types of graph. However, as Gardner (1984, p. 91) notes, "The confusion of this term with the 'graphs' of analytic geometry is regrettable, but the term has stuck [in the mathematical community]." In this work, the term "graph" will therefore be used to refer to a collection of vertices and edges, while a graph in the sense of a plot of a function will be called a "function graph" when any ambiguity arises.

Two- and three-dimensional graphs can be produced in the Wolfram Language using the commands Plot[f, {" src="https://mathworld.wolfram.com/images/equations/FunctionGraph/Inline13.gif" style="height:15px; width:5px" />x, xmin, xmin}" src="https://mathworld.wolfram.com/images/equations/FunctionGraph/Inline14.gif" style="height:15px; width:5px" />] and Plot3D[f, {" src="https://mathworld.wolfram.com/images/equations/FunctionGraph/Inline15.gif" style="height:15px; width:5px" />x, xmin, xmin}" src="https://mathworld.wolfram.com/images/equations/FunctionGraph/Inline16.gif" style="height:15px; width:5px" />, {" src="https://mathworld.wolfram.com/images/equations/FunctionGraph/Inline17.gif" style="height:15px; width:5px" />y, ymin, ymax}" src="https://mathworld.wolfram.com/images/equations/FunctionGraph/Inline18.gif" style="height:15px; width:5px" />], respectively.

Several examples of continuous functions which are notoriously difficult to graph are shown above: 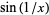 and its fractional part. Good routines for plotting graphs use adaptive algorithms which plot more points in regions where the function varies most rapidly (Wagon 1991, Math Works 1992, Heck 1993, Wickham-Jones 1994). Tupper (1996) has developed an algorithm that rigorously proves the pixels it generates are "on" if and only if there exists a mathematical point within the region of space represented by that pixel that is a solution to the relation being graphed. Although this method attempts to produce graphs that satisfy strict mathematical relationships, the problem of graphing is ultimately intractable, so no fixed algorithm can produce correct graphs for arbitrary relations.

REFERENCES:

Cleveland, W. S. The Elements of Graphing Data, rev. ed. Summit, NJ: Hobart, 1994.

Gardner, M. The Sixth Book of Mathematical Games from Scientific American. Chicago, IL: University of Chicago Press, p. 91, 1984.

Heck, A. Introduction to Maple, 2nd ed. New York: Springer-Verlag, pp. 303-304, 1993.

Math Works. Matlab Reference Guide. Natick, MA: The Math Works, p. 216, 1992.

Tufte, E. R. The Visual Display of Quantitative Information. Cheshire, CN: Graphics Press, 1983.

Tufte, E. R. Envisioning Information. Cheshire, CN: Graphics Press, 1990.

Tupper, J. Graphing Equations with Generalized Interval Arithmetic. M.Sc. Thesis. Department of Computer Science. Toronto: University of Toronto, 1996. http://www.dgp.toronto.edu/~mooncake/msc.html.

Tupper, J. "GrafEq." http://www.peda.com/grafeq/.

Wagon, S. Mathematica in Action. New York: W. H. Freeman, pp. 24-25, 1991.

Weisstein, E. W. "Books about Graphing." http://www.ericweisstein.com/encyclopedias/books/Graphing.html.

Wickham-Jones, T. Computer Graphics with Mathematica. Santa Clara, CA: TELOS, pp. 579-584, 1994.

Yates, R. C. "Sketching." A Handbook on Curves and Their Properties. Ann Arbor, MI: J. W. Edwards, pp. 188-205, 1952.

اخر الاخبار

اخبار العتبة العباسية المقدسة

المجمع العلمي للقرآن الكريم يصدر الكتاب الثاني من سلسلة يخشى

قسم الشعائر يكرّم أصحاب المواكب المشاركة في إحياء ذكرى شهادة السيدة الزهراء (عليها السلام)

جامعة العميد تستقبل طلبة المراحل الأولى المقبولين ضمن كلياتها للعام الدراسي الجديد

سماحة السيد الصافي يكرّم طلبة حفظ القرآن الكريم المتفوّقين ويؤكّد دور التدبّر في الهداية والتكامل

المزيد

الآخبار الصحية

طبيب يكشف تأثير برودة الشتاء على النوم

دون أن تعلم.. 10 عادات يومية تسرع شيخوخة جسمك

تقرير: النيكوتين خطر على القلب مهما كانت الطريقة

أيهما أفضل لصحتك.. زبدة الفول السوداني أم النوتيلا؟

المزيد

الآخبار التكنلوجية

السعودية تدشن أكبر نظام لتخزين الكهرباء بالبطاريات في العالم !

بأمر تنفيذي.. ترامب يؤكد هدف عودة الأميركيين إلى القمر في عام 2028

بعيدا عن البشر.. "قتال جوي في الفضاء" بين أميركا والصين

كشف مذهل في قاع "برمودا" !

المزيد