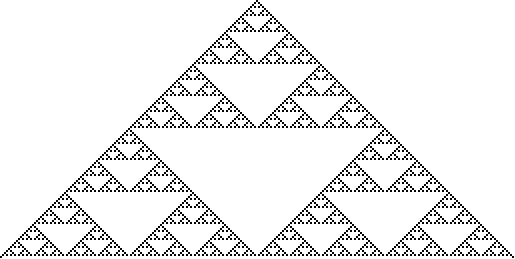
The Sierpiński sieve is a fractal described by Sierpiński in 1915 and appearing in Italian art from the 13th century (Wolfram 2002, p. 43). It is also called the Sierpiński gasket or Sierpiński triangle. The curve can be written as a Lindenmayer system with initial string "FXF--FF--FF", string rewriting rules "F" -> "FF", "X" -> "--FXF++FXF++FXF--", and angle .

The th iteration of the Sierpiński sieve is implemented in the Wolfram Language as SierpinskiMesh[n].

Let  be the number of black triangles after iteration ,  the length of a side of a triangle, and  the fractional area which is black after the th iteration. Then

			(1)
			(2)
			(3)

The capacity dimension is therefore

			(4)
			(5)
			(6)
			(7)

(OEIS A020857; Wolfram 1984; Borwein and Bailey 2003, p. 46).

The Sierpiński sieve is produced by the beautiful recurrence equation

(8)

where  denote bitwise XOR. It is also given by

(9)

where  is the st least significant bit defined by

(10)

and the product is taken over all  such that 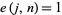 (Allouche and Shallit 2003, p. 113).

The Sierpinski sieve is given by Pascal's triangle (mod 2), giving the sequence 1; 1, 1; 1, 0, 1; 1, 1, 1, 1; 1, 0, 0, 0, 1; ... (OEIS A047999; left figure). In other words, coloring all odd numbers black and even numbers white in Pascal's triangle produces a Sierpiński sieve (Guy 1990; Wolfram 2002, p. 870; middle figure). The binomial coefficient 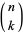 mod 2 can be computed using bitwise operations AND(NOT(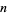), ), 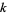giving the sequence 0; 0, 0; 0, 1, 0; 0, 0, 0, 0; 0, 1, 2, 3, 0; ... (OEIS A102037; right figure), then coloring the triangle black if the result is 0 and white otherwise. This is a consequence of the Lucas correspondence theorem for binomial coefficients modulo a prime number.

Surprisingly, elementary cellular automaton rules 60, 90 and 102 (when omitting the trailing zeros) also produce the Sierpinski sieve (Wolfram 2002, p. 870). Wolfram (2002, pp. 931-932) gives a large number of algorithms that can be used to compute a Sierpiński sieve.

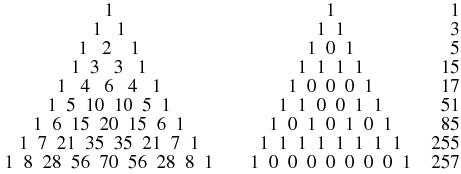
Gardner (1977) and independently Watkins (Conway and Guy 1996, Krížek et al. 2001) noticed that the number of sides for constructible polygons with odd Numbers of sides are given by the first 32 rows of the Sierpiński sieve interpreted as binary numbers, giving 1, 3, 5, 15, 17, 51, 85, 255, ... (OEIS A004729, Conway and Guy 1996, p. 140). In other words, every row is a product of distinct Fermat primes, with terms given by binary counting.

REFERENCES:

Allouche, J.-P. and Shallit, J. Automatic Sequences: Theory, Applications, Generalizations. Cambridge, England: Cambridge University Press, 2003.

Borwein, J. and Bailey, D. "Pascal's Triangle." §2.1 in Mathematics by Experiment: Plausible Reasoning in the 21st Century. Wellesley, MA: A K Peters, pp. 94-95, 2003.

Bulaevsky, J. "The Sierpinski Triangle Fractal." http://ejad.best.vwh.net/java/fractals/sierpinski.shtml.

Conway, J. H. and Guy, R. K. In The Book of Numbers. New York: Springer-Verlag, 1996.

Crandall, R. and Pomerance, C. Prime Numbers: A Computational Perspective, 2nd ed. New York: Springer-Verlag, 2005.

Crownover, R. M. Introduction to Fractals and Chaos. Sudbury, MA: Jones & Bartlett, 1995.

Dickau, R. M. "Two-Dimensional L-Systems." http://mathforum.org/advanced/robertd/lsys2d.html.

Dickau, R. M. "Typeset Fractals." Mathematica J. 7, 15, 1997.

Dickau, R. "Sierpinski-Menger Sponge Code and Graphic." http://library.wolfram.com/infocenter/Demos/4662/.

Gardner, M. "Pascal's Triangle." Ch. 15 in Mathematical Carnival: A New Round-Up of Tantalizers and Puzzles from Scientific American. New York: Vintage Books, pp. 194-207, 1977.

Guy, R. K. "The Second Strong Law of Small Numbers." Math. Mag. 63, 3-20, 1990.

Harris, J. W. and Stocker, H. "Sierpinski Gasket." §4.11.7 in Handbook of Mathematics and Computational Science. New York: Springer-Verlag, p. 115, 1998.

Kabai, S. Mathematical Graphics I: Lessons in Computer Graphics Using Mathematica. Püspökladány, Hungary: Uniconstant, p. 127, 2002.

Krížek, M.; Luca, F.; and Somer, L. 17 Lectures on Fermat Numbers: From Number Theory to Geometry. New York: Springer-Verlag, 2001.

Lauwerier, H. Fractals: Endlessly Repeated Geometric Figures. Princeton, NJ: Princeton University Press, pp. 13-14, 1991.

Mandelbrot, B. B. The Fractal Geometry of Nature. New York: W. H. Freeman, p. 142, 1983.

Peitgen, H.-O.; Jürgens, H.; and Saupe, D. Chaos and Fractals: New Frontiers of Science. New York: Springer-Verlag, pp. 78-88, 1992.

Peitgen, H.-O. and Saupe, D. (Eds.). The Science of Fractal Images. New York: Springer-Verlag, p. 282, 1988.

Sierpiński, W. "Sur une courbe dont tout point est un point de ramification." C. R. A. S. 160, 302-305, 1915.

Simmt, E. and Davis, B. "Fractal Cards: A Space for Exploration in Geometry and Discrete Mathematics." Math. Teacher 91, 102-108, 1998.

Sloane, N. J. A. Sequences A004729, A020857, A047999, and A102037 in "The On-Line Encyclopedia of Integer Sequences."

Steward, I. "Four Encounters with Sierpiński's Gasket." Math. Intel. 17, pp. 52-64, 1995.

Sved, M. "Divisibility--with Visibility." Math. Intell. 10, 56-64, 1988.

Wagon, S. Mathematica in Action. New York: W. H. Freeman, pp. 108 and 151-153, 1991.

Wang, P. "Renderings." http://www.ugcs.caltech.edu/~peterw/portfolio/renderings/

Wolfram, S. "Computation Theory of Cellular Automata." Comm. Math. Phys. 96, 15-57, 1984.

Wolfram, S. A New Kind of Science. Champaign, IL: Wolfram Media, pp. 870 and 931-932, 2002.

اخر الاخبار

اخبار العتبة العباسية المقدسة

معهد القرآن الكريم النسوي ينظّم سفرة دينية إلى كربلاء المقدسة لطالبات الدورات القرآنية الصيفية

العتبة العباسية المقدسة تناقش مع هيأة الإعلام والاتصالات تسهيل عمل المؤسّسات الصحفية لتغطية زيارة عاشوراء

لليوم الخامس.. العتبة العباسية المقدسة تواصل إقامة مجلس عزائها المركزي في الصحن الشريف

قسم الشؤون الدينية يفتتح موكبًا لخدمة زائري مدينة كربلاء في شهر المحرم

المزيد

الآخبار الصحية

لمن تجاوز الستين.. عليك بشرب 4 أكواب من القهوة يوميا ؟

الحليب مع العسل.. مزيج يمنحك 7 فوائد صحية

لا تبالغ في التنظيف.. قليل من "الاتساخ" قد يحمي عائلتك

دراسة تكشف علاقة خطيرة بين عمر الأم وصحة مولودها

المزيد

الآخبار التكنلوجية

هل هاتفك مراقب؟.. 5 علامات خطيرة تكشف التجسس عليك

دبي تطلق أول رحلة تجريبية للتاكسي الجوي

كيف تساعد الصيانة الوقائية في الحفاظ على كفاءة التكييف في سيارتك ؟

في ظاهرة غريبة حيرت العلماء.. كوكبنا قد يسجل أقصر يوم في التاريخ هذا الصيف!

المزيد