

تاريخ الرياضيات

الاعداد و نظريتها

تاريخ التحليل

تار يخ الجبر

الهندسة و التبلوجي


الرياضيات في الحضارات المختلفة

العربية

اليونانية

البابلية

الصينية

المايا

المصرية

الهندية


الرياضيات المتقطعة

المنطق

اسس الرياضيات

فلسفة الرياضيات

مواضيع عامة في المنطق


الجبر

الجبر الخطي

الجبر المجرد

الجبر البولياني

مواضيع عامة في الجبر

الضبابية

نظرية المجموعات

نظرية الزمر

نظرية الحلقات والحقول

نظرية الاعداد

نظرية الفئات

حساب المتجهات

المتتاليات-المتسلسلات

المصفوفات و نظريتها

المثلثات


الهندسة

الهندسة المستوية

الهندسة غير المستوية

مواضيع عامة في الهندسة

التفاضل و التكامل


المعادلات التفاضلية و التكاملية

معادلات تفاضلية

معادلات تكاملية

مواضيع عامة في المعادلات


التحليل

التحليل العددي

التحليل العقدي

التحليل الدالي

مواضيع عامة في التحليل

التحليل الحقيقي

التبلوجيا

نظرية الالعاب

الاحتمالات و الاحصاء

نظرية التحكم

بحوث العمليات

نظرية الكم

الشفرات

الرياضيات التطبيقية

نظريات ومبرهنات


علماء الرياضيات

500AD

500-1499

1000to1499

1500to1599

1600to1649

1650to1699

1700to1749

1750to1779

1780to1799

1800to1819

1820to1829

1830to1839

1840to1849

1850to1859

1860to1864

1865to1869

1870to1874

1875to1879

1880to1884

1885to1889

1890to1894

1895to1899

1900to1904

1905to1909

1910to1914

1915to1919

1920to1924

1925to1929

1930to1939

1940to the present

علماء الرياضيات

الرياضيات في العلوم الاخرى

بحوث و اطاريح جامعية

هل تعلم

طرائق التدريس

الرياضيات العامة

نظرية البيان
Fractal
المؤلف:
Barnsley, M. F. and Rising, H
المصدر:
Fractals Everywhere, 2nd ed. Boston, MA: Academic Press, 1993
الجزء والصفحة:
...
18-9-2021
2087
Fractal

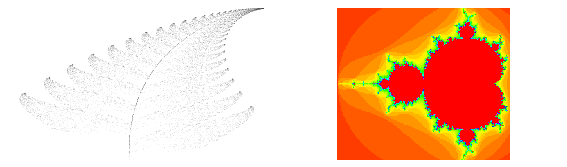
A fractal is an object or quantity that displays self-similarity, in a somewhat technical sense, on all scales. The object need not exhibit exactly the same structure at all scales, but the same "type" of structures must appear on all scales. A plot of the quantity on a log-log graph versus scale then gives a straight line, whose slope is said to be the fractal dimension. The prototypical example for a fractal is the length of a coastline measured with different length rulers. The shorter the ruler, the longer the length measured, a paradox known as the coastline paradox.
Illustrated above are the fractals known as the Gosper island, Koch snowflake, box fractal, Sierpiński sieve, Barnsley's fern, and Mandelbrot set.
REFERENCES:
Barnsley, M. F. and Rising, H. Fractals Everywhere, 2nd ed. Boston, MA: Academic Press, 1993.
Bogomolny, A. "Fractal Curves and Dimension." http://www.cut-the-knot.org/do_you_know/dimension.shtml.
Brandt, C.; Graf, S.; and Zähle, M. (Eds.). Fractal Geometry and Stochastics. Boston, MA: Birkhäuser, 1995.
Bunde, A. and Havlin, S. (Eds.). Fractals and Disordered Systems, 2nd ed. New York: Springer-Verlag, 1996.
Bunde, A. and Havlin, S. (Eds.). Fractals in Science. New York: Springer-Verlag, 1994.
Devaney, R. L. Complex Dynamical Systems: The Mathematics Behind the Mandelbrot and Julia Sets. Providence, RI: Amer. Math. Soc., 1994.
Devaney, R. L. and Keen, L. Chaos and Fractals: The Mathematics Behind the Computer Graphics. Providence, RI: Amer. Math. Soc., 1989.
Edgar, G. A. (Ed.). Classics on Fractals. Reading, MA: Addison-Wesley, 1993.
Eppstein, D. "Fractals." http://www.ics.uci.edu/~eppstein/junkyard/fractal.html.
Falconer, K. J. The Geometry of Fractal Sets, 1st pbk. ed., with corr. Cambridge, England: Cambridge University Press, 1986.
Feder, J. Fractals. New York: Plenum Press, 1988.
Giffin, N. "The Spanky Fractal Database." http://spanky.triumf.ca/www/welcome1.html.
Hastings, H. M. and Sugihara, G. Fractals: A User's Guide for the Natural Sciences. New York: Oxford University Press, 1994.
Kaye, B. H. A Random Walk Through Fractal Dimensions, 2nd ed. New York: Wiley, 1994.
Lauwerier, H. A. Fractals: Endlessly Repeated Geometrical Figures. Princeton, NJ: Princeton University Press, 1991.
le Méhaute, A. Fractal Geometries: Theory and Applications. Boca Raton, FL: CRC Press, 1992.
Mandelbrot, B. B. Fractals: Form, Chance, & Dimension. San Francisco, CA: W. H. Freeman, 1977.
Mandelbrot, B. B. The Fractal Geometry of Nature. New York: W. H. Freeman, 1983.
Massopust, P. R. Fractal Functions, Fractal Surfaces, and Wavelets. San Diego, CA: Academic Press, 1994.
Pappas, T. "Fractals--Real or Imaginary." The Joy of Mathematics. San Carlos, CA: Wide World Publ./Tetra, pp. 78-79, 1989.
Peitgen, H.-O.; Jürgens, H.; and Saupe, D. Chaos and Fractals: New Frontiers of Science. New York: Springer-Verlag, 1992.
Peitgen, H.-O.; Jürgens, H.; and Saupe, D. Fractals for the Classroom, Part 1: Introduction to Fractals and Chaos. New York: Springer-Verlag, 1992.
Peitgen, H.-O. and Richter, D. H. The Beauty of Fractals: Images of Complex Dynamical Systems. New York: Springer-Verlag, 1986.
Peitgen, H.-O. and Saupe, D. (Eds.). The Science of Fractal Images. New York: Springer-Verlag, 1988.
Pickover, C. A. (Ed.). The Pattern Book: Fractals, Art, and Nature. World Scientific, 1995.
Pickover, C. A. (Ed.). Fractal Horizons: The Future Use of Fractals. New York: St. Martin's Press, 1996.
Rietman, E. Exploring the Geometry of Nature: Computer Modeling of Chaos, Fractals, Cellular Automata, and Neural Networks. New York: McGraw-Hill, 1989.
Russ, J. C. Fractal Surfaces. New York: Plenum, 1994.
Schroeder, M. Fractals, Chaos, Power Law: Minutes from an Infinite Paradise. New York: W. H. Freeman, 1991.
Sprott, J. C. "Sprott's Fractal Gallery." http://sprott.physics.wisc.edu/fractals.htm.
Stauffer, D. and Stanley, H. E. From Newton to Mandelbrot, 2nd ed. New York: Springer-Verlag, 1995.
Stevens, R. T. Fractal Programming in C. New York: Henry Holt, 1989.
Takayasu, H. Fractals in the Physical Sciences. Manchester, England: Manchester University Press, 1990.
Taylor, M. C. and Louvet, J.-P. "sci.fractals FAQ." http://www.faqs.org/faqs/sci/fractals-faq/.
Tricot, C. Curves and Fractal Dimension. New York: Springer-Verlag, 1995.
Triumf Mac Fractal Programs. http://spanky.triumf.ca/pub/fractals/programs/MAC/.
Vicsek, T. Fractal Growth Phenomena, 2nd ed. Singapore: World Scientific, 1992.
Weisstein, E. W. "Books about Fractals." http://www.ericweisstein.com/encyclopedias/books/Fractals.html.
Yamaguti, M.; Hata, M.; and Kigami, J. Mathematics of Fractals. Providence, RI: Amer. Math. Soc., 1997.
 الاكثر قراءة في الرياضيات التطبيقية
الاكثر قراءة في الرياضيات التطبيقية
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام) قسم الشؤون الفكرية يصدر مجموعة قصصية بعنوان (قلوب بلا مأوى)
قسم الشؤون الفكرية يصدر مجموعة قصصية بعنوان (قلوب بلا مأوى)


















