Log Normal Distribution

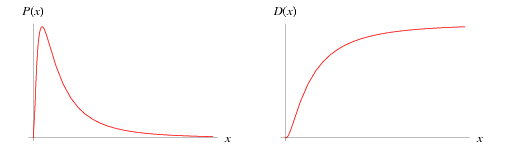
A continuous distribution in which the logarithm of a variable has a normal distribution. It is a general case of Gibrat's distribution, to which the log normal distribution reduces with 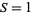 and 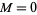. A log normal distribution results if the variable is the product of a large number of independent, identically-distributed variables in the same way that a normal distribution results if the variable is the sum of a large number of independent, identically-distributed variables.

The probability density and cumulative distribution functions for the log normal distribution are

			(1)
			(2)

where 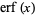 is the erf function.

It is implemented in the Wolfram Language as LogNormalDistribution[mu, sigma].

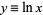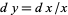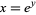This distribution is normalized, since letting  gives  and , so

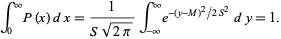(3)

The raw moments are

			(4)
			(5)
			(6)
			(7)

and the central moments are

			(8)
			(9)
			(10)

Therefore, the mean, variance, skewness, and kurtosis excess are given by

			(11)
			(12)
			(13)
			(14)

These can be found by direct integration

			(15)
			(16)
			(17)

and similarly for .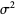

Examples of variates which have approximately log normal distributions include the size of silver particles in a photographic emulsion, the survival time of bacteria in disinfectants, the weight and blood pressure of humans, and the number of words written in sentences by George Bernard Shaw.

REFERENCES:

Aitchison, J. and Brown, J. A. C. The Lognormal Distribution, with Special Reference to Its Use in Economics. New York: Cambridge University Press, 1957.

Balakrishnan, N. and Chen, W. W. S. Handbook of Tables for Order Statistics from Lognormal Distributions with Applications. Amsterdam, Netherlands: Kluwer, 1999.

Crow, E. L. and Shimizu, K. (Ed.). Lognormal Distributions:Theory and Applications. New York: Dekker, 1988.

Kenney, J. F. and Keeping, E. S. Mathematics of Statistics, Pt. 2, 2nd ed. Princeton, NJ: Van Nostrand, p. 123, 1951.