Given a function 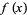 of a variable  tabulated at 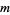 values 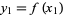, ..., 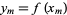, assume the function is of known analytic form depending on  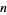parameters 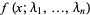, and consider the overdetermined set of  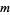equations

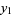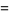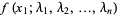			(1)
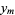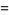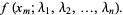			(2)

We desire to solve these equations to obtain the values 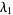, ...,  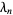which best satisfy this system of equations. Pick an initial guess for the  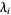and then define

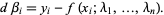(3)

Now obtain a linearized estimate for the changes 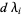 needed to reduce  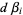to 0,

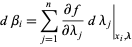(4)

for 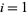, ..., 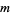, where 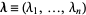. This can be written in component form as

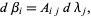(5)

where 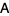 is the  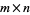matrix

(6)

In more concise matrix form,

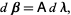(7)

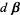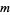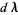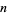where  is an -vector and  is an -vector.

Applying the transpose of 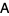 to both sides gives

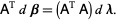(8)

Defining

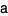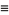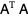			(9)
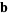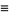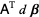			(10)

in terms of the known quantities 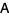 and 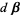 then gives the matrix equation

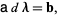(11)

which can be solved for 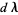 using standard matrix techniques such as Gaussian elimination. This offset is then applied to  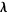and a new  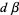is calculated. By iteratively applying this procedure until the elements of  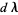become smaller than some prescribed limit, a solution is obtained. Note that the procedure may not converge very well for some functions and also that convergence is often greatly improved by picking initial values close to the best-fit value. The sum of square residuals is given by  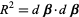after the final iteration.

An example of a nonlinear least squares fit to a noisy Gaussian function

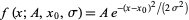(12)

is shown above, where the thin solid curve is the initial guess, the dotted curves are intermediate iterations, and the heavy solid curve is the fit to which the solution converges. The actual parameters are 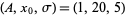, the initial guess was (0.8, 15, 4), and the converged values are (1.03105, 20.1369, 4.86022), with 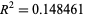. The partial derivatives used to construct the matrix  are

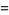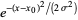			(13)
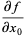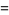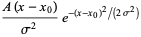			(14)
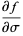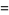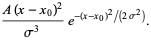			(15)

The technique could obviously be generalized to multiple Gaussians, to include slopes, etc., although the convergence properties generally worsen as the number of free parameters is increased.

An analogous technique can be used to solve an overdetermined set of equations. This problem might, for example, arise when solving for the best-fit Euler angles corresponding to a noisy rotation matrix, in which case there are three unknown angles, but nine correlated matrix elements. In such a case, write the 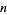 different functions as  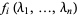for 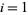, ..., 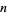, call their actual values 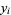, and define

(16)

and

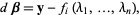(17)

where 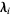 are the numerical values obtained after the 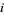th iteration. Again, set up the equations as

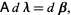(18)

and proceed exactly as before.

REFERENCES:

Bates, D. M. and Watts, D. G. Nonlinear Regression and Its Applications. New York: Wiley, 1988.

اخر الاخبار

اخبار العتبة العباسية المقدسة

شعبة الحرم تُجري حملة تنظيفٍ بعد انتهاء زيارة العاشر من المحرم

تطبيق (إعلامي) يحصد المرتبة الأولى ضمن أفضل التطبيقات المجّانية

خَدَمة العتبة العباسية المقدسة يؤدّون مراسم الممارسة العبادية بالتزامن مع ذكرى عاشوراء

المجمع العلمي يختتم مجالس العزاء لليالي العشر الأولى من المحرّم في بغداد

المزيد

الآخبار الصحية

تناول الجبن.. مفيد للجسم أم خطر يهدد صحتك؟

طبيبة أسنان تحذر.. لا تتجاهل هذه العلامة بعد التنظيف

يجب أن تأكل المزيد من الشمام هذا الصيف.. إليك السبب ؟

تأثير صحي كبير.. كم بيضة يجب أن تتناول يوميا؟

المزيد

الآخبار التكنلوجية

أداء خلايا البيروفسكايت الشمسية تحت الماء قد يزيد كفاءة تحويل الكهرباء

مسافة الأمان: أساس القيادة الآمنة وتجنب الحوادث

هل القيادة السريعة تعني استهلاك اكثر للوقود؟

لماذا يعتبر كوكب المريخ غير صالح للحياة؟

المزيد