
Wigner,s Semicircle Law
 المؤلف:
Bai, Z. D. and Yin, Y. Q.
المؤلف:
Bai, Z. D. and Yin, Y. Q.
 المصدر:
"Convergence to the Semicircle Law." Ann. Probab. 16
المصدر:
"Convergence to the Semicircle Law." Ann. Probab. 16
 الجزء والصفحة:
...
الجزء والصفحة:
...
 23-3-2021
23-3-2021
 4332
4332
Wigner's Semicircle Law
Let 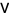 be a real symmetric matrix of large order
be a real symmetric matrix of large order 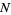 having random elements
having random elements 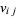 that for
that for 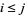 are independently distributed with equal densities, equal second moments
are independently distributed with equal densities, equal second moments 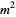 , and
, and 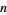 th moments bounded by constants
th moments bounded by constants 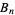 independent of
independent of 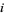 ,
, 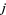 , and
, and 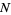 . Further, let
. Further, let 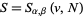 be the number of eigenvalues of
be the number of eigenvalues of 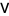 that lie in the interval
that lie in the interval 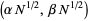 for real
for real 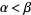 . Then
. Then
(Wigner 1955, 1958). This law was first observed by Wigner (1955) for certain special classes of random matrices arising in quantum mechanical investigations.

The distribution of eigenvalues of a symmetric random matrix with entries chosen from a standard normal distribution is illustrated above for a random 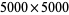 matrix.
matrix.
Note that a large real symmetric matrix with random entries taken from a uniform distribution also obeys the semicircle law with the exception that it also possesses exactly one large eigenvalue.
REFERENCES:
Arnold, L. "On Wigner's Semicircle Law for the Eigenvalues of Random Matrices." Z. Wahrscheinlichkeitstheorie und Verw. Gebiete 19, 191-198, 1971.
Bai, Z. D. and Yin, Y. Q. "Convergence to the Semicircle Law." Ann. Probab. 16, 863-875, 1988.
Götze, F. and Tikhomirov, A. "Rate of Convergence to the Semi-Circular Law." Probab. Theory Related Fields 127, 228-276, 2003.
Kiessling, M. K.-H. and Spohn, H. "A Note on the Eigenvalue Density of Random Matrices." Comm. Math. Phys. 199, 683-695, 1999.
Ryan, Ø. "On the Limit Distributions of Random Matrices with Independent or Free Entries." Comm. Math. Phys. 193, 595-626, 1998.
Voiculescu, D. "Limit Laws for Random Matrices and Free Products." Invent. Math. 104, 201-220, 1991.
Wigner, E. "Characteristic Vectors of Bordered Matrices with Infinite Dimensions." Ann. of Math. 62, 548-564, 1955.
Wigner, E. "On the Distribution of the Roots of Certain Symmetric Matrices." Ann. of Math. 67, 325-328, 1958.
 الاكثر قراءة في الاحتمالات و الاحصاء
الاكثر قراءة في الاحتمالات و الاحصاء
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


