Coin Tossing

An idealized coin consists of a circular disk of zero thickness which, when thrown in the air and allowed to fall, will rest with either side face up ("heads" H or "tails" T) with equal probability. A coin is therefore a two-sided die. Despite slight differences between the sides and nonzero thickness of actual coins, the distribution of their tosses makes a good approximation to a 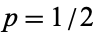 Bernoulli distribution.

There are, however, some rather counterintuitive properties of coin tossing. For example, it is twice as likely that the triple TTH will be encountered before THT than after it, and three times as likely that THH will precede HHT. Furthermore, it is six times as likely that HTT will be the first of HTT, TTH, and TTT to occur than either of the others (Honsberger 1979). There are also strings 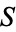 of Hs and Ts that have the property that the expected wait  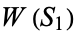to see string  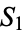is less than the expected wait  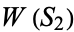to see 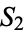, but the probability of seeing  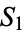before seeing  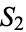is less than 1/2 (Gardner 1988, Berlekamp et al. 2001). Examples include

1. THTH and HTHH, for which 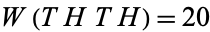 and 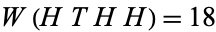, but for which the probability that THTH occurs before HTHH is 9/14 (Gardner 1988, p. 64),

2. 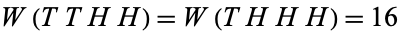, , but for which the probability that TTHH occurs before HHH is 7/12, and for which the probability that THHH occurs before HHH is 7/8 (Penney 1969; Gardner 1988, p. 66).

More amazingly still, spinning a penny instead of tossing it results in heads only about 30% of the time (Paulos 1995).

The study of runs of two or more identical tosses is well-developed, but a detailed treatment is surprisingly complicated given the simple nature of the underlying process. For example, the probability that no two consecutive tails will occur in  tosses is given by , where  is a Fibonacci number. Similarly, the probability that no  consecutive tails will occur in  tosses is given by 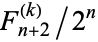, where  is a Fibonacci k-step number.

Toss a fair coin over and over, record the sequence of heads and tails, and consider the number of tosses needed such that all possible sequences of heads and tails of length 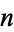 occur as subsequences of the tosses. The minimum number of tosses is  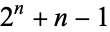(Havil 2003, p. 116), giving the first few terms as 2, 5, 10, 19, 36, 69, 134, ... (OEIS A052944). The minimal sequences for  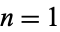are HT and TH, and for  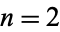are HHTTH, HTTHH, THHTT, and TTHHT. The numbers of distinct minimal toss sequences for 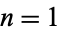, 2, ... are 2, 4, 16, 256, ... (OEIS A001146), which appear to simply be .

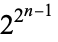It is conjectured that as 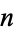 becomes large, the average number of tosses needed to get all subsequences of length  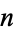is 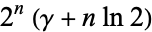, where  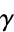is the Euler-Mascheroni constant (Havil 2003, p. 116).

REFERENCES:

Berlekamp, E. R.; Conway, J. H; and Guy, R. K. Winning Ways for Your Mathematical Plays, Vol. 1: Adding Games, 2nd ed. Wellesley, MA: A K Peters, p. 777, 2001.

Ford, J. "How Random is a Coin Toss?" Physics Today 36, 40-47, 1983.

Gardner, M. "Nontransitive Paradoxes." Time Travel and Other Mathematical Bewilderments. New York: W. H. Freeman, pp. 64-66, 1988.

Havil, J. Gamma: Exploring Euler's Constant. Princeton, NJ: Princeton University Press, 2003.

Honsberger, R. "Some Surprises in Probability." Ch. 5 in Mathematical Plums (Ed. R. Honsberger). Washington, DC: Math. Assoc. Amer., pp. 100-103, 1979.

Keller, J. B. "The Probability of Heads." Amer. Math. Monthly 93, 191-197, 1986.

Paulos, J. A. A Mathematician Reads the Newspaper. New York: BasicBooks, p. 75, 1995.

Peterson, I. Islands of Truth: A Mathematical Mystery Cruise. New York: W. H. Freeman, pp. 238-239, 1990.

Penney, W. "Problem 95. Penney-Ante." J. Recr. Math. 2, 241, 1969.

Sloane, N. J. A. Sequences A000225/M2655, A001146/M1297, A050227, and A052944 in "The On-Line Encyclopedia of Integer Sequences."

Spencer, J. "Combinatorics by Coin Flipping." Coll. Math. J., 17, 407-412, 1986.

Whittaker, E. T. and Robinson, G. "The Frequency Distribution of Tosses of a Coin." §90 in The Calculus of Observations: A Treatise on Numerical Mathematics, 4th ed. New York: Dover, pp. 176-177, 1967.