FM Modulation

Light passing through an electro-optic phase modulator will be up- or downshifted in frequency unless it passes through at the time when the intracavity phase modulator δ(t) is stationary at either of its extrema. The recirculating energy passing through the phase modulator at any other time receives a Doppler shift proportional to dδ/dt, and the repeated Doppler shifts on successive passes through the modulator eventually push this energy outside the frequency band over which gain is available from the laser medium. The interaction of the spectrally widened circulating power with the narrow laser linewidth leads to a reduction in gain for most frequency components. Thus, the effect of the phase modulator is similar to the loss modulator, and the previous discussion of loss modulation also applies here. The existence of two phase extrema per period creates a phase uncertainty in the mode-locked pulse position since the pulse can occur at either of two equally probable phases relative to the modulating signal. The quadratic variation of δ(t) about the pulse arrival time also produces a frequency “chirp” within the short mode-locked pulses.
In the FM case, the internal FM introduces a sinusoidally varying phase perturbation such that the round-trip transmission through the modulator is given approximately by

........(1)

where δ_FM is the peak phase retardation through the modulator. The ± sign corresponds to the two possible phase positions at which the pulse can pass through the modulator, as mentioned earlier. With these parameters the pulse width of phase mode-locked pulses is given by

........(2)

The time-bandwidth product is given by

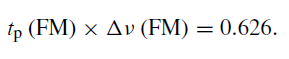........(3)

In an electro-optic phase modulator the phase retardation is proportional to the modulating voltage, hence δFM ∝ P^1/2_in , where Pin is the drive power into the modulator. Therefore, we obtain from (2) the following expression for the pulse width: tp(FM) ∝ P^−1/8_in , which indicates that the pulses shorten very slowly with increased modulator drive. More effective in shortening the pulses is an increase of the modulation frequency. Since ν_m = c/2L, the pulse width will be proportional to the square root of the cavity length.

In order to calculate the pulse width from (2), we can calculate the saturated gain coefficient g by equating the loop gain with the loss in the resonator

.......(4)

where R is the effective reflectivity of the output mirror and includes all losses.
For a typical Nd :YAG laser with 10% round-trip loss, that is, R = 0.9, a resonator length of 60 cm, and a linewidth of 120 GHz, the pulse length is given by t_p(FM) = 39(1/δ_FM)^1/4. For δ_FM = 1 rad, which is easily obtainable, pulses of 39 ps can be generated.