First-Order Reactions

We have seen earlier that the rate law of a generic first-order reaction where A → B can be expressed in terms of the reactant concentration:

Rate of reaction = – [latex] frac{Delta [A]}{Delta t} [/latex] = [latex] extit{k}[A]{}^{1} [/latex]

This form of the rate law is sometimes referred to as the differential rate law. We can perform a mathematical procedure known as an integration to transform the rate law to another useful form known as the integrated rate law:

ln [latex] frac{{[A]}_t}{{[A]}_0} [/latex]= –[latex] extit{k}t [/latex]

where “ln” is the natural logarithm, [A]₀ is the initial concentration of A, and [A]_t is the concentration of A at another time.

The process of integration is beyond the scope of this textbook, but is covered in most calculus textbooks and courses. The most useful aspect of the integrated rate law is that it can be rearranged to have the general form of a straight line (y = mx + b).

ln [latex] {[A]}_t [/latex]= –[latex] extit{k}t + ln {[A]}_0 [/latex]

(y = mx + b)

Therefore, if we were to graph the natural logarithm of the concentration of a reactant (ln) versus time, a reaction that has a first-order rate law will yield a straight line, while a reaction with any other order will not yield a straight line (Figure 17.7 “Concentration vs. Time, First-Order Reaction”). The slope of the straight line corresponds to the negative rate constant, –k, and the y-intercept corresponds to the natural logarithm of the initial concentration.

Figure 17.7. Concentration vs. Time, First-Order Reaction

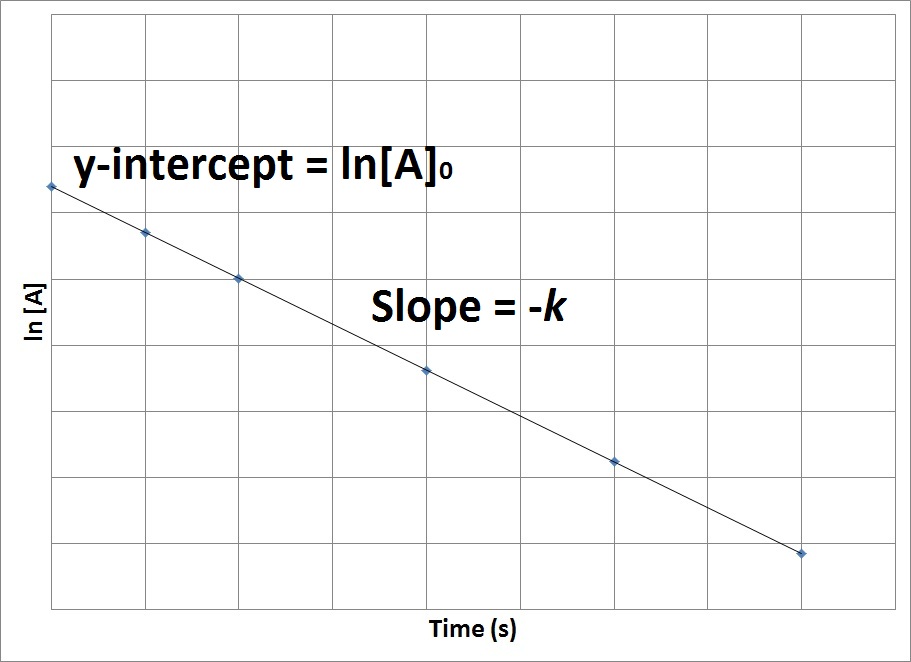
This graph shows the plot of the natural logarithm of concentration versus time for a first-order reaction.