
تاريخ الفيزياء

علماء الفيزياء


الفيزياء الكلاسيكية

الميكانيك

الديناميكا الحرارية


الكهربائية والمغناطيسية

الكهربائية

المغناطيسية

الكهرومغناطيسية


علم البصريات

تاريخ علم البصريات

الضوء

مواضيع عامة في علم البصريات

الصوت


الفيزياء الحديثة


النظرية النسبية

النظرية النسبية الخاصة

النظرية النسبية العامة

مواضيع عامة في النظرية النسبية

ميكانيكا الكم

الفيزياء الذرية

الفيزياء الجزيئية


الفيزياء النووية

مواضيع عامة في الفيزياء النووية

النشاط الاشعاعي


فيزياء الحالة الصلبة

الموصلات

أشباه الموصلات

العوازل

مواضيع عامة في الفيزياء الصلبة

فيزياء الجوامد


الليزر

أنواع الليزر

بعض تطبيقات الليزر

مواضيع عامة في الليزر


علم الفلك

تاريخ وعلماء علم الفلك

الثقوب السوداء


المجموعة الشمسية

الشمس

كوكب عطارد

كوكب الزهرة

كوكب الأرض

كوكب المريخ

كوكب المشتري

كوكب زحل

كوكب أورانوس

كوكب نبتون

كوكب بلوتو

القمر

كواكب ومواضيع اخرى

مواضيع عامة في علم الفلك

النجوم

البلازما

الألكترونيات

خواص المادة


الطاقة البديلة

الطاقة الشمسية

مواضيع عامة في الطاقة البديلة

المد والجزر

فيزياء الجسيمات


الفيزياء والعلوم الأخرى

الفيزياء الكيميائية

الفيزياء الرياضية

الفيزياء الحيوية

الفيزياء العامة


مواضيع عامة في الفيزياء

تجارب فيزيائية

مصطلحات وتعاريف فيزيائية

وحدات القياس الفيزيائية

طرائف الفيزياء

مواضيع اخرى
Diurnal and planetary aberration
المؤلف:
A. Roy, D. Clarke
المصدر:
Astronomy - Principles and Practice 4th ed
الجزء والصفحة:
p 137
5-8-2020
2758
Diurnal and planetary aberration
The rotation of the Earth on its axis produces aberration in an amount large enough to be taken into account in precise observational work.
Let an observer be at a place of latitude ∅ and let R⊕, c and T be the Earth’s radius, the velocity of light and the number of seconds in one sidereal day. Then the observer O has velocity v due to the Earth’s rotation, given by
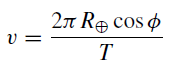
as easily seen by figure 1.
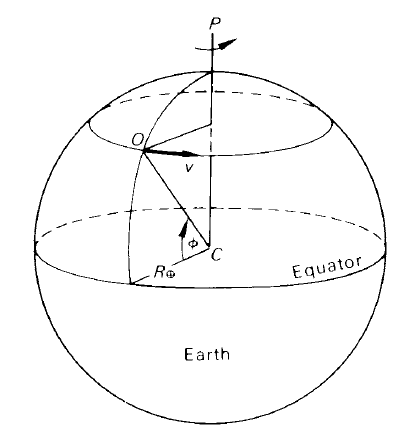
Figure 1. The velocity of an observer due to the rotation of the Earth.
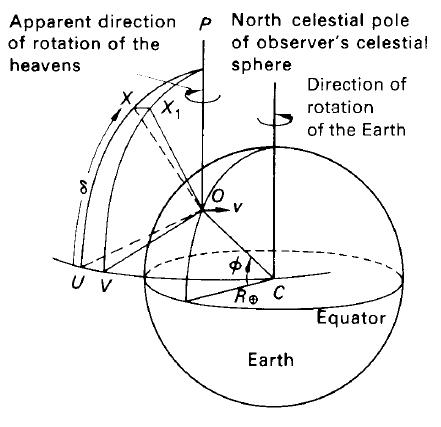
Figure 2. The effect of diurnal aberration.
The constant of diurnal aberration κ1 is then given in seconds of arc by
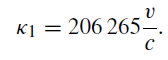
Evaluating, it is found that
κ1 = 0''·32 cos ∅. (1)
Let us consider an observation made of a star of declination δ when it crosses the meridian. As the observer moves in an easterly direction due to the Earth’s rotation, diurnal aberration will cause the star to be seen east of its geocentric position. The star’s observed time of transit is, therefore, late by an amount Δt, obtained in the following way.
The star’s position at apparent transit is X1 (figure 2) but its true position is X, where
XX1 ≈ 0''·32 cos ∅.
Now if XX1 is an arc of the star’s parallel of declination,
XX1 = UV cos δ.
But UV is the delay in transit time since it is the difference in the hour angles of X and X1. Hence, the delay time Δt is given by
Δt = UV = XX1 sec δ = 0''·32 cosφ sec δ
that is
Δt = 0·s021 cos∅ sec δ.
The declinations at transit, and, therefore, the meridian zenith distances, of the stars are not affected by diurnal aberration.
In the case of planets, the light entering the terrestrial observer’s eye comes from the direction the planet occupied at the epoch t0 at which the light left the planet. In addition to the normal correction for stellar and diurnal aberration, therefore, a further correction is required to obtain the planet’s direction at the epoch t1 at which it is observed. The time interval (t1−t0) is obtained from the planet’s geocentric distance divided by the velocity of light. If dα/dt and dδ/dt are the rates of change in geocentric right ascension and declination of the planet then the required corrections due to planetary aberration are given by (t1 − t0) dα/dt and (t1 − t0) dδ/dt.
It may also be mentioned in passing that in the case of an artificial Earth satellite with an orbital velocity of order 7 km s−1, the aberration in its observed position is of order 5 arc sec and must be allowed for in precise tracking.
 الاكثر قراءة في مواضيع عامة في علم الفلك
الاكثر قراءة في مواضيع عامة في علم الفلك
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















