Spherical geometry

The geometry of the sphere is made up of great circles, small circles and arcs of these figures. Distances
along great circles are often measured as angles since, for convenience, the radius of the sphere is made
unity.
A great circle is defined to be the intersection with the sphere of a plane containing the centre of the sphere. Since the centre is equidistant from all points on the sphere, the figure of intersection must be a circle by definition. If the plane does not contain the centre of the sphere, its intersection with the sphere is a small circle.
In figure 1, ABCDA is a great circle. If two points P and Q are chosen to be 90◦ away from all points on the great circle (by drawing the diameter POQ perpendicular to the plane ABCDA), they are said to be the poles of the great circle ABCDA.
The small circle EFGHE was obtained by choosing a point K on the diameter PQ and letting the plane through K and perpendicular to PQ cut the sphere. It is easily shown that the figure produced by this procedure is a circle.
Let PFBQP be any great circle through the poles P and Q. Then, by the construction of EFGH, KF is perpendicular to OK, so that the triangle KFO is right-angled at K. By Pythagoras,

OF² = OK² + KF²....... (1)

But OF and OK are both constant (OF is a radius of the sphere and OK is a constant) and, therefore, by equation (1), KF is constant.

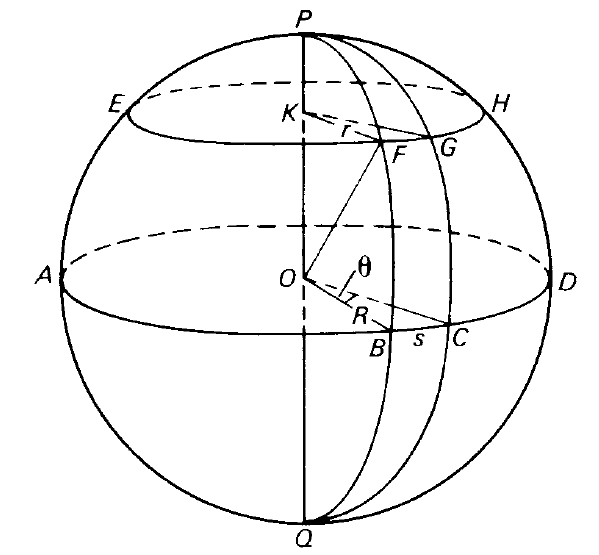
Figure 1. The basis of spherical geometry.

By construction, F is any point on figure EFGHE so that all points on EFGHE must be equidistant from K. Since they also lie on a plane, EFGHE must be a circle, centre K. P and Q are also the poles of circle EFGHE. Draw another great circle PGCQP through the poles P and Q to intersect the small circle EFGHE and great circle ABCDA in G and C respectively.
Then the angle between the tangents at P to the great circles PFBQP and PGCQP is said to be the spherical angle at P or angle GPF or angle CPB. A spherical angle is defined only with reference to two intersecting great circles. If three great circles intersect one another so that a closed figure is formed by three arcs of the great circles, it is called a spherical triangle provided that it possesses the following properties:
1. Any two sides are together greater than the third side.
2. The sum of the three angles is greater than 180◦.
3. Each spherical angle is less than 180◦.
In figure 1, therefore, figure PBC is an example of a spherical triangle but figure PFG is not, the latter being excluded because one of its sides (FG) is the arc of a small circle. It may be noted in passing that ΔPBC is a special case where two of the angles, namely ∠PBC and ∠PCB, are right
angles.
The sides of a spherical triangle are expressed in angular measure.
The length s of the arc BC is given in terms of the angle θ it subtends at the centre of the sphere
and the sphere’s radius R by the relation

s = R × θ

where θ is expressed in radians.
It should be remembered that
 

2π radians = 360 degrees.
 

Other useful relationships are:

If the radius of the sphere is taken as unity,
 

s = θ
 

showing that the length of a great circle arc on a sphere of unit radius is equal to the angle (in circular measure) subtended by this arc at the centre of the sphere.
The length of a small circle arc, such as FG, is related simply to the length of an arc of the great circle whose plane is parallel to that of the small circle.
In figure 1, let r be the radius of the small circle EFGHE. Then
FG = r × ∠FKG.
Also
BC = R × ∠BOC.
Both OB and KF lie on plane PFBQ; KF also lies on plane EFGH while OB lies on plane ABCD . Therefore, KF must be parallel to OB, since plane EFGH is parallel to plane ABCD. Similarly, KG is parallel to OC. Then
∠FKG = ∠BOC.
Hence,
FG = BC × r/R

In the plane triangle KOF, right-angled at K, KF = r ; OF = R. Hence,
FG = BC × sinKOF.
But ∠POB = 90◦ so that we may write alternatively
FG = BC cos FB.
If the radius of the sphere is unity,
PF = ∠POF = ∠KOF
and
FB = ∠FOB,
so that we have
FG = BC sin PF
and

FG = BC cos FB................. (2)

اخر الاخبار

اخبار العتبة العباسية المقدسة

قسم الإعلام يشارك في الاجتماع التحضيري لمناقشة الخطة الإعلامية لزيارة عاشوراء

بحضور متوليها الشرعي.. العتبة العباسية المقدسة تواصل إقامة المجالس الحسينية لإحياء شهر المحرم

قسم الشؤون الفكرية يطلق برنامجه التبليغي في أكثر من 20 دولة إفريقية

شعبتا الخطابة النسوية والتوجيه الديني تواصلان إقامة المجالس الحسينية في مرقد أبي الفضل العباس (عليه السلام)

المزيد

الآخبار الصحية

دراسة تكشف علاقة خطيرة بين عمر الأم وصحة مولودها

دراسة تحذر.. اضطراب نوم بسيط قد يسبب الموت المبكر ؟

الاستحمام بالماء الساخن.. راحة مؤقتة وأضرار دائمة للبشرة

ماذا يحدث للجسم عند تخطي وجبة الإفطار؟

المزيد

الآخبار التكنلوجية

كيف تساعد الصيانة الوقائية في الحفاظ على كفاءة التكييف في سيارتك ؟

في ظاهرة غريبة حيرت العلماء.. كوكبنا قد يسجل أقصر يوم في التاريخ هذا الصيف!

السد الصيني العملاق يعيق دوران الأرض ويغيّر شكلها ؟

السعودية تطلق 10 تجارب علمية إلى محطة الفضاء الدولية

المزيد

مواضيع ذات صلة

اختبار الانفجار الهائل

الكوسمولوجيا وأشكال كالابي - ياو

التخمينات الكوسمولوجيا والنظرية النهائية

اختبار الانفجار الهائل

النموذج القياسي للكوسمولوجيا، أو علم الكون

تأملات في علم الكون

المذنبات

الصعود إلى الفضاء

اختلاف الليل والنهار

تصنيع الصاروخ و اطلاقة

الكويكبات والمذنبات

صورة الحجر الأزتكي (فهم وإدراك الحضارة الآزيتية )