آخر المواضيع المضافة

 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 1-1-2021
Date: 23-10-2019
Date: 6-10-2020
|
Linnik's constant 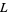 is the constant appearing in Linnik's theorem. Heath-Brown (1992) has shown that
is the constant appearing in Linnik's theorem. Heath-Brown (1992) has shown that 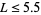 , and Schinzel, Sierpiński, and Kanold (Ribenboim 1989) have conjectured that
, and Schinzel, Sierpiński, and Kanold (Ribenboim 1989) have conjectured that 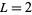 .
.
REFERENCES:
Finch, S. R. "Linnik's Constant." §2.12 in Mathematical Constants. Cambridge, England: Cambridge University Press, pp. 127-130, 2003.
Guy, R. K. Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, p. 13, 1994.
Heath-Brown, D. R. "Zero-Free Regions for Dirichlet 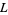 -Functions and the Least Prime in an Arithmetic Progression." Proc. London Math. Soc. 64, 265-338, 1992.
-Functions and the Least Prime in an Arithmetic Progression." Proc. London Math. Soc. 64, 265-338, 1992.
Ribenboim, P. The New Book of Prime Number Records. New York: Springer-Verlag, 1989.



|
|
|
|
4 أسباب تجعلك تضيف الزنجبيل إلى طعامك.. تعرف عليها
|
|
|
|
|
|
|
أكبر محطة للطاقة الكهرومائية في بريطانيا تستعد للانطلاق
|
|
|
|
|
|
|
العتبة العباسية المقدسة تبحث مع العتبة الحسينية المقدسة التنسيق المشترك لإقامة حفل تخرج طلبة الجامعات
|
|
|