The series

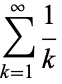(1)

is called the harmonic series. It can be shown to diverge using the integral test by comparison with the function 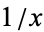. The divergence, however, is very slow. Divergence of the harmonic series was first demonstrated by Nicole d'Oresme (ca. 1323-1382), but was mislaid for several centuries (Havil 2003, p. 23; Derbyshire 2004, pp. 9-10). The result was proved again by Pietro Mengoli in 1647, by Johann Bernoulli in 1687, and by Jakob Bernoulli shortly thereafter (Derbyshire 2004, pp. 9-10).

Progressions of the form

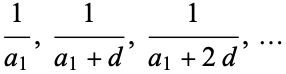(2)

are also sometimes called harmonic series (Beyer 1987).

Oresme's proof groups the harmonic terms by taking 2, 4, 8, 16, ... terms (after the first two) and noting that each such block has a sum larger than 1/2,

			(3)
			(4)

and since an infinite sum of 1/2's diverges, so does the harmonic series.

The generalization of the harmonic series

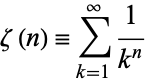(5)

is known as the Riemann zeta function.

The sum of the first few terms of the harmonic series is given analytically by the 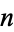th harmonic number

			(6)
			(7)

where 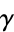 is the Euler-Mascheroni constant and  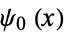is the digamma function.

The only values of 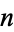 for which  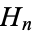is a regular number are 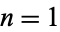, 2, and 6 (Havil 2003, pp. 24-25).

The number of terms needed for 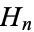 to exceed 1, 2, 3, ... are 1, 4, 11, 31, 83, 227, 616, 1674, 4550, 12367, 33617, 91380, 248397, ... (OEIS A004080; DeTemple and Wang 1991). Using the analytic form shows that after  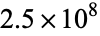terms, the sum is still less than 20. Furthermore, to achieve a sum greater than 100, more than  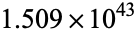terms are needed! Written explicitly, the number of terms is

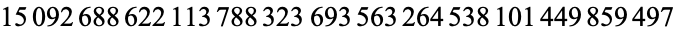(8)

(Boas and Wrench 1971; Gardner 1984, p. 167). More generally, the number of terms needed to equal or exceed 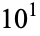, , 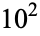, 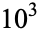... are 12367, 15092688622113788323693563264538101449859497, 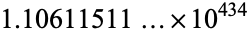, ... (OEIS A096618).

The harmonic series of primes

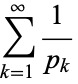(9)

taken over all primes 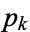 also diverges (Wells 1986, p. 41) with asymptotic behavior

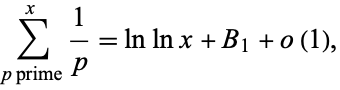(10)

(Hardy 1999, p. 50), where 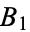 is the Mertens constant.

Rather surprisingly, the alternating series

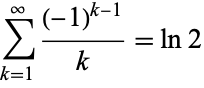(11)

converges to the natural logarithm of 2. An explicit formula for the partial sum of the alternating series is given by

(12)

Gardner (1984) notes that this series never reaches an integer sum.

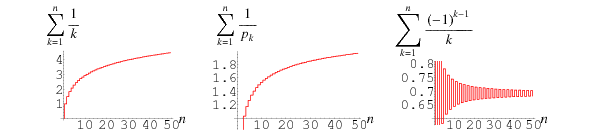
The partial sums of the harmonic series are plotted in the left figure above, together with two related series.

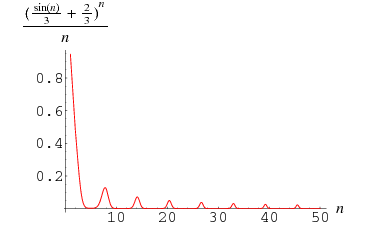
It is not known if the series

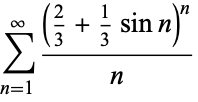(13)

converges (Borwein et al. 2004, p. 56). After 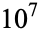 terms, the series equals approximately 2.163.

REFERENCES:

Arfken, G. Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 279-280, 1985.

Atanassov, K. T. 'Notes on the Harmonic Series." Bull. Number Th. Related Topics 10, 10-20, 1986.

Beyer, W. H. (Ed.). CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, p. 8, 1987.

Boas, R. P. and Wrench, J. W. "Partial Sums of the Harmonic Series." Amer. Math. Monthly 78, 864-870, 1971.

Borwein, J.; Bailey, D.; and Girgensohn, R. Experimentation in Mathematics: Computational Paths to Discovery. Wellesley, MA: A K Peters, 2004.

Derbyshire, J. Prime Obsession: Bernhard Riemann and the Greatest Unsolved Problem in Mathematics. New York: Penguin, pp. 8-9, 2004.

DeTemple, D. W. and Wang, S.-H. "Half Integer Approximations for the Partial Sums of the Harmonic Series." J. Math. Anal. Appl. 160, 149-156, 1991.

Gardner, M. The Sixth Book of Mathematical Games from Scientific American. Chicago, IL: University of Chicago Press, pp. 165-172, 1984.

Hardy, G. H. Ramanujan: Twelve Lectures on Subjects Suggested by His Life and Work, 3rd ed. New York: Chelsea, 1999.

Havil, J. "The Harmonic Series." Ch. 2 in Gamma: Exploring Euler's Constant. Princeton, NJ: Princeton University Press, pp. 21-25, 2003.

Hoffman, P. The Man Who Loved Only Numbers: The Story of Paul Erdős and the Search for Mathematical Truth. New York: Hyperion, p. 217, 1998.

Honsberger, R. "An Intriguing Series." Ch. 10 in Mathematical Gems II. Washington, DC: Math. Assoc. Amer., pp. 98-103, 1976.

Rosenbaum, B. "Solution to Problem E46." Amer. Math. Monthly 41, 48, 1934.

Shutler, P. M. E. "Euler's Constant, Stirling's Approximation and the Riemann Zeta Function." Internat. J. Math. Ed. Sci. Tech. 28, 677-688, 1997.

Sloane, N. J. A. Sequence A004080 in "The On-Line Encyclopedia of Integer Sequences."

Wells, D. The Penguin Dictionary of Curious and Interesting Numbers. Middlesex, England: Penguin Books, p. 41, 1986.

اخر الاخبار

اخبار العتبة العباسية المقدسة

ضمن جهوده المتواصلة.. قسم الشؤون الخدمية ينفذ حملة غسل وتنظيف لمحيط العتبة العباسية المقدسة

قسم الشؤون الفكرية يختتم مسابقة نجم الأئمة (عليهم السلام) بنسختها الخامسة في بغداد

المجمع العلمي يواصل الختمة القرآنية الرمضانية المرتلة حفظًا في مقام الإمام المهدي (عجَّل الله فرجه)

الحلقة 26 من جائزة العميد القرآنية تشهد مشاركة 5 قراء من الفتية ضمن المرحلة النهائية

المزيد

الآخبار الصحية

دراسة: تناول القهوة يوميا يخفض خطر الإصابة بالاضطرابات النفسية

عرض شائع في الفم قد يكون مرتبطا بخطر الإصابة بأمراض خطيرة

نصائح عامة لاستخدام سماعات الرأس بأمان

تأثير اللياقة البدنية على الدماغ

المزيد

الآخبار التكنلوجية

ديدان الأرض تكشف تلوث التربة بالمعادن الثقيلة

خبير أرصاد جوية: ظاهرة النينيو القادمة قد تكون الأقوى خلال 10 سنوات

"ناسا" تكشف موعد إعادة إطلاق رحلتها المأهولة إلى القمر

علماء الجيولوجيا يفكون لغز الصدع العملاق تحت الماء في المحيط الأطلسي

المزيد