Jacobi Polynomial

The Jacobi polynomials, also known as hypergeometric polynomials, occur in the study of rotation groups and in the solution to the equations of motion of the symmetric top. They are solutions to the Jacobi differential equation, and give some other special named polynomials as special cases. They are implemented in the Wolfram Language as JacobiP[n, a, b, z].

For 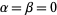,  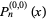reduces to a Legendre polynomial. The Gegenbauer polynomial

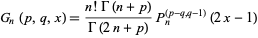(1)

and Chebyshev polynomial of the first kind can also be viewed as special cases of the Jacobi polynomials.

Plugging

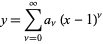(2)

into the Jacobi differential equation gives the recurrence relation

(3)

for 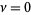, 1, ..., where

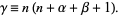(4)

Solving the recurrence relation gives

(5)

for 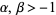. They form a complete orthogonal system in the interval  with respect to the weighting function

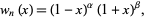(6)

and are normalized according to

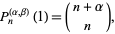(7)

where 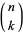 is a binomial coefficient. Jacobi polynomials can also be written

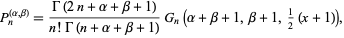(8)

where 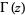 is the gamma function and

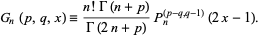(9)

Jacobi polynomials are orthogonal polynomials and satisfy

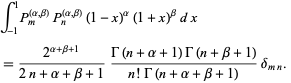(10)

The coefficient of the term 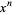 in 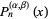 is given by

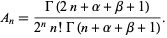(11)

They satisfy the recurrence relation

(12)

where 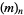 is a Pochhammer symbol

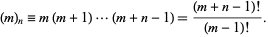(13)

The derivative is given by

(14)

The orthogonal polynomials with weighting function 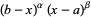 on the closed interval  can be expressed in the form

(15)

(Szegö 1975, p. 58).

Special cases with  are

			(16)
			(17)
			(18)
			(19)

Further identities are

			(20)
			(21)

(22)

(Szegö 1975, p. 79).

The kernel polynomial is

(23)

(Szegö 1975, p. 71).

The polynomial discriminant is

(24)

(Szegö 1975, p. 143).

In terms of the hypergeometric function,

			(25)
			(26)
			(27)

where 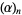 is the Pochhammer symbol (Abramowitz and Stegun 1972, p. 561; Koekoek and Swarttouw 1998).

Let 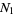 be the number of zeros in 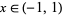,  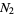the number of zeros in 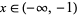, and 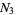 the number of zeros in 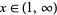. Define Klein's symbol

(28)

where 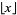 is the floor function, and

			(29)
			(30)
			(31)

If the cases 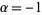, , 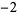..., 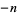, , 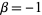, 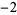..., 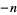, and 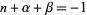, , 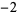...,  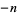are excluded, then the number of zeros of  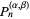in the respective intervals are

			(32)
			(33)
			(34)

(Szegö 1975, pp. 144-146), where 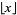 is again the floor function.

The first few polynomials are

			(35)
			(36)
			(37)

(Abramowitz and Stegun 1972, p. 793).

See Abramowitz and Stegun (1972, pp. 782-793) and Szegö (1975, Ch. 4) for additional identities.

REFERENCES:

Abramowitz, M. and Stegun, I. A. (Eds.). "Orthogonal Polynomials." Ch. 22 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 771-802, 1972.

Andrews, G. E.; Askey, R.; and Roy, R. "Jacobi Polynomials and Gram Determinants" and "Generating Functions for Jacobi Polynomials." §6.3 and 6.4 in Special Functions. Cambridge, England: Cambridge University Press, pp. 293-306, 1999.

Iyanaga, S. and Kawada, Y. (Eds.). "Jacobi Polynomials." Appendix A, Table 20.V in Encyclopedic Dictionary of Mathematics. Cambridge, MA: MIT Press, p. 1480, 1980.

Koekoek, R. and Swarttouw, R. F. "Jacobi." §1.8 in The Askey-Scheme of Hypergeometric Orthogonal Polynomials and its 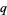-Analogue. Delft, Netherlands: Technische Universiteit Delft, Faculty of Technical Mathematics and Informatics Report 98-17, pp. 38-44, 1998.

Roman, S. "The Theory of the Umbral Calculus I." J. Math. Anal. Appl. 87, 58-115, 1982.

Szegö, G. "Jacobi Polynomials." Ch. 4 in Orthogonal Polynomials, 4th ed. Providence, RI: Amer. Math. Soc., 1975.