
Chebyshev Polynomial of the Second Kind
 المؤلف:
Abramowitz, M. and Stegun, I. A.
المؤلف:
Abramowitz, M. and Stegun, I. A.
 المصدر:
"Orthogonal Polynomials." Ch. 22 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover
المصدر:
"Orthogonal Polynomials." Ch. 22 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover
 الجزء والصفحة:
...
الجزء والصفحة:
...
 3-8-2019
3-8-2019
 4687
4687
Chebyshev Polynomial of the Second Kind
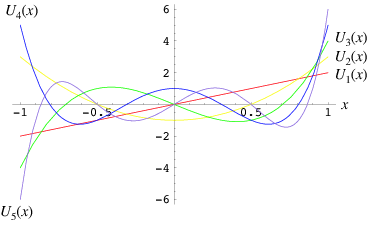
A modified set of Chebyshev polynomials defined by a slightly different generating function. They arise in the development of four-dimensional spherical harmonics in angular momentum theory. They are a special case of the Gegenbauer polynomial with 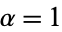 . They are also intimately connected with trigonometric multiple-angle formulas. The Chebyshev polynomials of the second kind are denoted
. They are also intimately connected with trigonometric multiple-angle formulas. The Chebyshev polynomials of the second kind are denoted 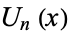 , and implemented in the Wolfram Language as ChebyshevU[n, x]. The polynomials
, and implemented in the Wolfram Language as ChebyshevU[n, x]. The polynomials 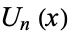 are illustrated above for
are illustrated above for ![x in [-1,1]](http://mathworld.wolfram.com/images/equations/ChebyshevPolynomialoftheSecondKind/Inline4.gif) and
and 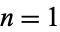 , 2, ..., 5.
, 2, ..., 5.
The first few Chebyshev polynomials of the second kind are
When ordered from smallest to largest powers, the triangle of nonzero coefficients is 1; 2; 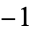 , 4;
, 4; 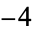 , 8; 1,
, 8; 1, 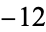 , 16; 6,
, 16; 6, 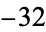 , 32; ... (OEIS A053117).
, 32; ... (OEIS A053117).
The defining generating function of the Chebyshev polynomials of the second kind is
for 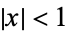 and
and 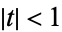 . To see the relationship to a Chebyshev polynomial of the first kind
. To see the relationship to a Chebyshev polynomial of the first kind 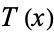 , take
, take 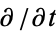 of equation (9) to obtain
of equation (9) to obtain
Multiplying (◇) by 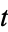 then gives
then gives
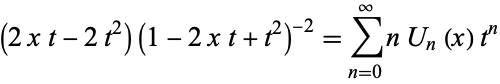 |
(12)
|
and adding (12) and (◇) gives
This is the same generating function as for the Chebyshev polynomial of the first kind except for an additional factor of 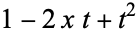 in the denominator.
in the denominator.
The Rodrigues representation for 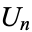 is
is
![U_n(x)=((-1)^n(n+1)sqrt(pi))/(2^(n+1)(n+1/2)!(1-x^2)^(1/2))(d^n)/(dx^n)[(1-x^2)^(n+1/2)].](http://mathworld.wolfram.com/images/equations/ChebyshevPolynomialoftheSecondKind/NumberedEquation2.gif) |
(15)
|
The polynomials can also be defined in terms of the sums
where 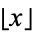 is the floor function and
is the floor function and ![[x]](http://mathworld.wolfram.com/images/equations/ChebyshevPolynomialoftheSecondKind/Inline63.gif) is the ceiling function, or in terms of the product
is the ceiling function, or in terms of the product
![U_n(x)=2^nproduct_(k=1)^n[x-cos((kpi)/(n+1))]](http://mathworld.wolfram.com/images/equations/ChebyshevPolynomialoftheSecondKind/NumberedEquation3.gif) |
(18)
|
(Zwillinger 1995, p. 696).
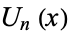 also obey the interesting determinant identity
also obey the interesting determinant identity
 |
(19)
|
The Chebyshev polynomials of the second kind are a special case of the Jacobi polynomials 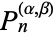 with
with 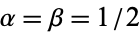 ,
,
where 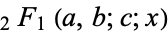 is a hypergeometric function (Koekoek and Swarttouw 1998).
is a hypergeometric function (Koekoek and Swarttouw 1998).
Letting 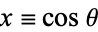 allows the Chebyshev polynomials of the second kind to be written as
allows the Chebyshev polynomials of the second kind to be written as
![U_n(x)=(sin[(n+1)theta])/(sintheta).](http://mathworld.wolfram.com/images/equations/ChebyshevPolynomialoftheSecondKind/NumberedEquation5.gif) |
(22)
|
The second linearly dependent solution to the transformed differential equation is then given by
![W_n(x)=(cos[(n+1)theta])/(sintheta),](http://mathworld.wolfram.com/images/equations/ChebyshevPolynomialoftheSecondKind/NumberedEquation6.gif) |
(23)
|
which can also be written
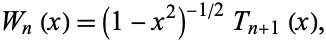 |
(24)
|
where 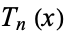 is a Chebyshev polynomial of the first kind. Note that
is a Chebyshev polynomial of the first kind. Note that 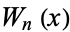 is therefore not a polynomial.
is therefore not a polynomial.
The triangle of resultants 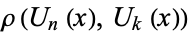 is given by
is given by ![<span style=]() {0}" src="http://mathworld.wolfram.com/images/equations/ChebyshevPolynomialoftheSecondKind/Inline78.gif" style="height:14px; width:17px" />,
{0}" src="http://mathworld.wolfram.com/images/equations/ChebyshevPolynomialoftheSecondKind/Inline78.gif" style="height:14px; width:17px" />, ![<span style=]() {-4,0}" src="http://mathworld.wolfram.com/images/equations/ChebyshevPolynomialoftheSecondKind/Inline79.gif" style="height:14px; width:42px" />,
{-4,0}" src="http://mathworld.wolfram.com/images/equations/ChebyshevPolynomialoftheSecondKind/Inline79.gif" style="height:14px; width:42px" />, ![<span style=]() {0,-64,0}" src="http://mathworld.wolfram.com/images/equations/ChebyshevPolynomialoftheSecondKind/Inline80.gif" style="height:14px; width:64px" />,
{0,-64,0}" src="http://mathworld.wolfram.com/images/equations/ChebyshevPolynomialoftheSecondKind/Inline80.gif" style="height:14px; width:64px" />, ![<span style=]() {16,256,4096,0}" src="http://mathworld.wolfram.com/images/equations/ChebyshevPolynomialoftheSecondKind/Inline81.gif" style="height:14px; width:104px" />,
{16,256,4096,0}" src="http://mathworld.wolfram.com/images/equations/ChebyshevPolynomialoftheSecondKind/Inline81.gif" style="height:14px; width:104px" />, ![<span style=]() {0,0,0,1048576,0}" src="http://mathworld.wolfram.com/images/equations/ChebyshevPolynomialoftheSecondKind/Inline82.gif" style="height:14px; width:123px" />, ... (OEIS A054376).
{0,0,0,1048576,0}" src="http://mathworld.wolfram.com/images/equations/ChebyshevPolynomialoftheSecondKind/Inline82.gif" style="height:14px; width:123px" />, ... (OEIS A054376).
REFERENCES:
Abramowitz, M. and Stegun, I. A. (Eds.). "Orthogonal Polynomials." Ch. 22 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 771-802, 1972.
Arfken, G. "Chebyshev (Tschebyscheff) Polynomials" and "Chebyshev Polynomials--Numerical Applications." §13.3 and 13.4 in Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 731-748, 1985.
Koekoek, R. and Swarttouw, R. F. "Chebyshev." §1.8.2 in The Askey-Scheme of Hypergeometric Orthogonal Polynomials and its 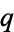 -Analogue. Delft, Netherlands: Technische Universiteit Delft, Faculty of Technical Mathematics and Informatics Report 98-17, pp. 41-43, 1998.
-Analogue. Delft, Netherlands: Technische Universiteit Delft, Faculty of Technical Mathematics and Informatics Report 98-17, pp. 41-43, 1998.
Koepf, W. "Efficient Computation of Chebyshev Polynomials." In Computer Algebra Systems: A Practical Guide (Ed. M. J. Wester). New York: Wiley, pp. 79-99, 1999.
Pegg, E. Jr. "ChebyshevU." http://www.mathpuzzle.com/ChebyshevU.html.
Rivlin, T. J. Chebyshev Polynomials. New York: Wiley, 1990.
Sloane, N. J. A. Sequences A053117 and A054376 in "The On-Line Encyclopedia of Integer Sequences."
Spanier, J. and Oldham, K. B. "The Chebyshev Polynomials 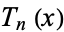 and
and 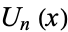 ." Ch. 22 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 193-207, 1987.
." Ch. 22 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 193-207, 1987.
Vasilyev, N. and Zelevinsky, A. "A Chebyshev Polyplayground: Recurrence Relations Applied to a Famous Set of Formulas." Quantum 10, 20-26, Sept./Oct. 1999.
Zwillinger, D. (Ed.). CRC Standard Mathematical Tables and Formulae. Boca Raton, FL: CRC Press, 1995.
 الاكثر قراءة في التفاضل و التكامل
الاكثر قراءة في التفاضل و التكامل
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


