d-Orbital Splittings

CFT focuses on the interaction of the five (n − 1)d orbitals with ligands arranged in a regular array around a transition-metal ion. We will focus on the application of CFT to octahedral complexes, which are by far the most common and the easiest to visualize. Other common structures, such as square planar complexes, can be treated as a distortion of the octahedral model. According to CFT, an octahedral metal complex forms because of the electrostatic interaction of a positively charged metal ion with six negatively charged ligands or with the negative ends of dipoles associated with the six ligands. In addition, the ligands interact with one other electrostatically. As you learned in our discussion of the valence-shell electron-pair repulsion (VSEPR) model, the lowest-energy arrangement of six identical negative charges is an octahedron, which minimizes repulsive interactions between the ligands.

We begin by considering how the energies of the d orbitals of a transition-metal ion are affected by an octahedral arrangement of six negative charges. Recall that the five d orbitals are initially degenerate (have the same energy). If we distribute six negative charges uniformly over the surface of a sphere, the d orbitals remain degenerate, but their energy will be higher due to repulsive electrostatic interactions between the spherical shell of negative charge and electrons in the d orbitals (Figure 1.1a

). Placing the six negative charges at the vertices of an octahedron does not change the average energy of the d orbitals, but it does remove their degeneracy: the five d orbitals split into two groups whose energies depend on their orientations. As shown in Figure 1.1b

, the d_z² and d_x²−y² orbitals point directly at the six negative charges located on the x, y, and z axes. Consequently, the energy of an electron in these two orbitals (collectively labeled the e_g orbitals) will be greater than it will be for a spherical distribution of negative charge because of increased electrostatic repulsions. In contrast, the other three d orbitals (d_xy, d_xz, and d_yz, collectively called the t_2g orbitals) are all oriented at a 45° angle to the coordinate axes, so they point between the six negative charges. The energy of an electron in any of these three orbitals is lower than the energy for a spherical distribution of negative charge.

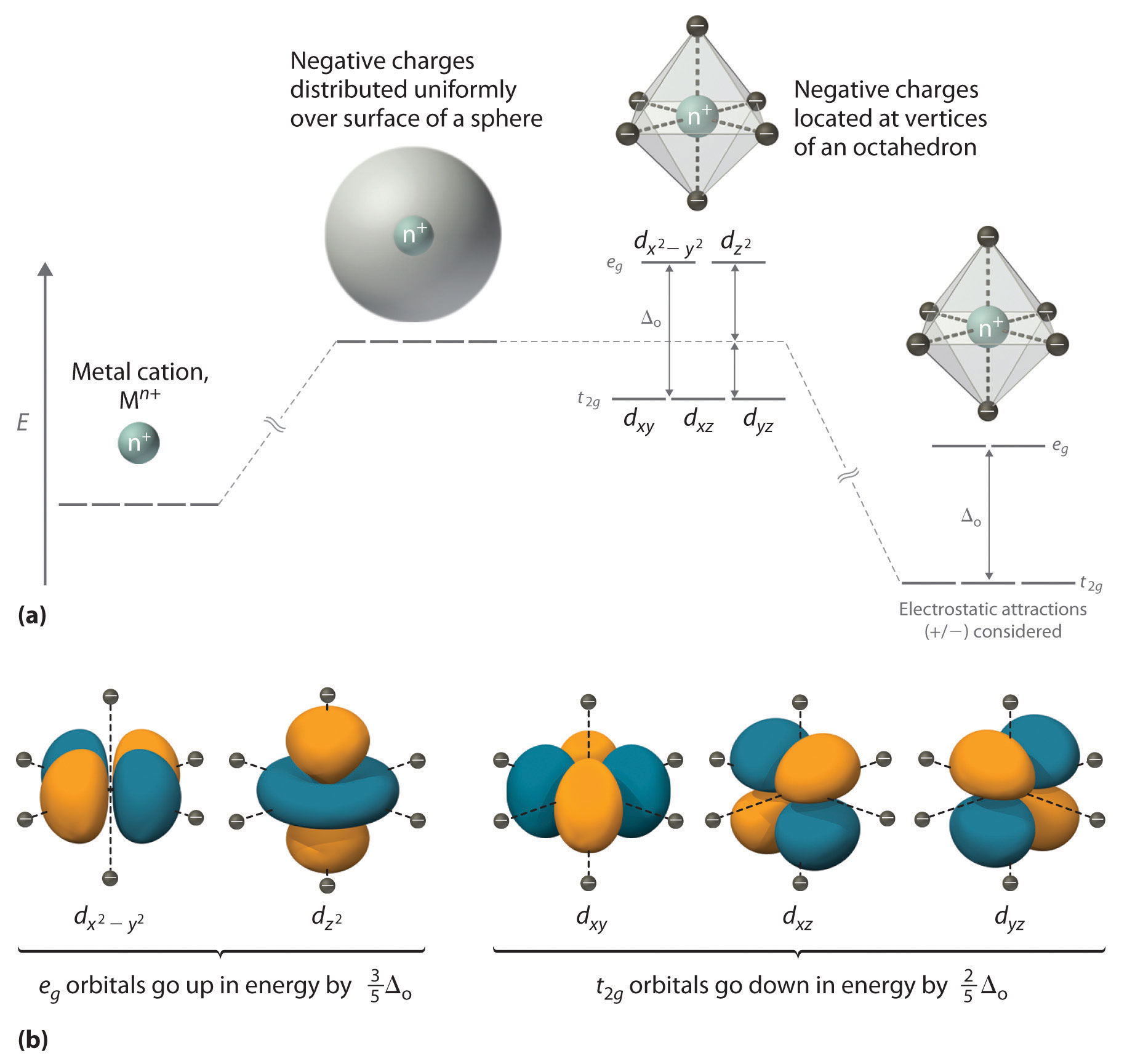
Figure 1.1 : An Octahedral Arrangement of Six Negative Charges around a Metal Ion Causes the Five d Orbitals to Split into Two Sets with Different Energies. (a) Distributing a charge of −6 uniformly over a spherical surface surrounding a metal ion causes the energy of all five d orbitals to increase due to electrostatic repulsions, but the five d orbitals remain degenerate. Placing a charge of −1 at each vertex of an octahedron causes the d orbitals to split into two groups with different energies: the d_x²−y² and d_z² orbitals increase in energy, while the, d_xy, d_xz, and d_yz orbitals decrease in energy. The average energy of the five d orbitals is the same as for a spherical distribution of a −6 charge, however. Attractive electrostatic interactions between the negatively charged ligands and the positively charged metal ion (far right) cause all five d orbitals to decrease in energy but does not affect the splittings of the orbitals. (b) The two e_g orbitals (left) point directly at the six negatively charged ligands, which increases their energy compared with a spherical distribution of negative charge. In contrast, the three t_2g orbitals (right) point between the negatively charged ligands, which decreases their energy compared with a spherical distribution of charge.

The difference in energy between the two sets of d orbitals is called the crystal field splitting energy (Δ_o), where the subscript o stands for octahedral. As we shall see, the magnitude of the splitting depends on the charge on the metal ion, the position of the metal in the periodic table, and the nature of the ligands. (Crystal field splitting energy also applies to tetrahedral complexes: Δ_t.) It is important to note that the splitting of the d orbitals in a crystal field does not change the total energy of the five d orbitals: the two e_g orbitals increase in energy by 0.6Δ_o, whereas the three t_2g orbitals decrease in energy by 0.4Δ_o. Thus the total change in energy is

Crystal field splitting does not change the total energy of the d orbitals.

Thus far, we have considered only the effect of repulsive electrostatic interactions between electrons in the d orbitals and the six negatively charged ligands, which increases the total energy of the system and splits the d orbitals. Interactions between the positively charged metal ion and the ligands results in a net stabilization of the system, which decreases the energy of all five d orbitals without affecting their splitting (as shown at the far right in Figure 1.1a).