Whipple,s Transformation
المؤلف:
Andrews, G. E. and Burge, W. H.
المصدر:
"Determinant Identities." Pacific J. Math. 158
الجزء والصفحة:
...
20-6-2019
1822
Whipple's Transformation
(Bailey 1935, p. 25), where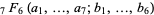 
and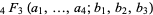 
are generalized hypergeometric functions with argument 
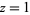and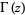 
is the gamma function.
Another transformation due to Whipple (1926ab) is given by
for one of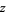 
and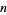 
a nonnegative integer (Andrews and Burge 1993).
REFERENCES:
Andrews, G. E. and Burge, W. H. "Determinant Identities." Pacific J. Math. 158, 1-14, 1993.
Bailey, W. N. Generalised Hypergeometric Series. Cambridge, England: Cambridge University Press, pp. 25 and 29, 1935.
Whipple, F. J. W. "On Well-Poised Series, Generalized Hypergeometric Series Having Parameters in Pairs, Each Pair with the Same Sum." Proc. London Math. Soc. 24, 247-263, 1926a.
Whipple, F. J. W. "Well-Poised Series and Other Generalized Hypergeometric Series." Proc. London Math. Soc. Ser. 2 25, 525-544, 1926b.
Whipple, F. J. W. "A Fundamental Relation Between Generalized Hypergeometric Series." Proc. London Math. Soc. 26, 257-272, 1927.
الاكثر قراءة في التفاضل و التكامل
اخر الاخبار
اخبار العتبة العباسية المقدسة
