Dougall-Ramanujan Identity
المؤلف:
Bailey, W. N.
المصدر:
"An Elementary Proof of Dougalls Theorem." §5.1 in Generalised Hypergeometric Series. Cambridge, England: Cambridge University Press
الجزء والصفحة:
...
22-5-2019
2002
Dougall-Ramanujan Identity
A hypergeometric identity discovered by Ramanujan around 1910. From Hardy (1999, pp. 13 and 102-103),
 |
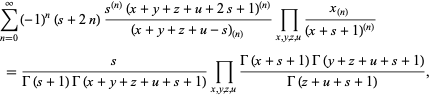(1)
|
where
 |
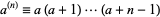(2)
|
is the rising factorial (a.k.a. Pochhammer symbol,
 |
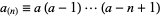(3)
|
is the falling factorial (Hardy 1999, p. 101),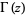 
is a gamma function, and one of
 |
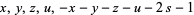(4)
|
is a positive integer.
Equation (1) can also be rewritten as
 |
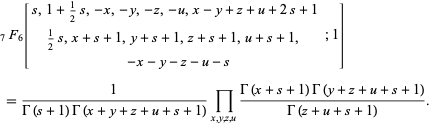(5)
|
(Hardy 1999, p. 102). In a more symmetric form, if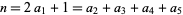 
, 
, 
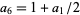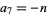, and 
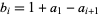for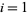 
, 2, ..., 6, then
 |
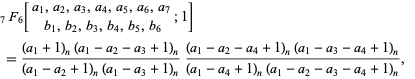(6)
|
where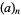 
is the Pochhammer symbol (Petkovšek et al. 1996).
The identity is a special case of Jackson's identity, and gives Dixon's theorem, Saalschütz's theorem, and Morley's formula as special cases.
REFERENCES:
Bailey, W. N. "An Elementary Proof of Dougall's Theorem." §5.1 in Generalised Hypergeometric Series. Cambridge, England: Cambridge University Press, pp. 25-26 and 34, 1935.
Dixon, A. C. "Summation of a Certain Series." Proc. London Math. Soc. 35, 285-289, 1903.
Dougall, J. "On Vandermonde's Theorem and Some More General Expansions." Proc. Edinburgh Math. Soc. 25, 114-132, 1907.
Hardy, G. H. "A Chapter from Ramanujan's Note-Book." Proc. Cambridge Philos. Soc. 21, 492-503, 1923.
Hardy, G. H. Ramanujan: Twelve Lectures on Subjects Suggested by His Life and Work, 3rd ed. New York: Chelsea, 1999.
Petkovšek, M.; Wilf, H. S.; and Zeilberger, D. A=B. Wellesley, MA: A K Peters, pp. 43, 126-127, and 183-184, 1996. http://www.cis.upenn.edu/~wilf/AeqB.html.
الاكثر قراءة في التفاضل و التكامل
اخر الاخبار
اخبار العتبة العباسية المقدسة
