

علم الكيمياء

تاريخ الكيمياء والعلماء المشاهير

التحاضير والتجارب الكيميائية

المخاطر والوقاية في الكيمياء

اخرى

مقالات متنوعة في علم الكيمياء

كيمياء عامة


الكيمياء التحليلية

مواضيع عامة في الكيمياء التحليلية

التحليل النوعي والكمي

التحليل الآلي (الطيفي)

طرق الفصل والتنقية


الكيمياء الحياتية

مواضيع عامة في الكيمياء الحياتية

الكاربوهيدرات

الاحماض الامينية والبروتينات

الانزيمات

الدهون

الاحماض النووية

الفيتامينات والمرافقات الانزيمية

الهرمونات


الكيمياء العضوية

مواضيع عامة في الكيمياء العضوية

الهايدروكاربونات

المركبات الوسطية وميكانيكيات التفاعلات العضوية

التشخيص العضوي

تجارب وتفاعلات في الكيمياء العضوية


الكيمياء الفيزيائية

مواضيع عامة في الكيمياء الفيزيائية

الكيمياء الحرارية

حركية التفاعلات الكيميائية

الكيمياء الكهربائية


الكيمياء اللاعضوية

مواضيع عامة في الكيمياء اللاعضوية

الجدول الدوري وخواص العناصر

نظريات التآصر الكيميائي

كيمياء العناصر الانتقالية ومركباتها المعقدة


مواضيع اخرى في الكيمياء

كيمياء النانو

الكيمياء السريرية

الكيمياء الطبية والدوائية

كيمياء الاغذية والنواتج الطبيعية

الكيمياء الجنائية


الكيمياء الصناعية

البترو كيمياويات

الكيمياء الخضراء

كيمياء البيئة

كيمياء البوليمرات

مواضيع عامة في الكيمياء الصناعية

الكيمياء الاشعاعية والنووية
Hexagonal Close-Packed and Cubic Close-Packed Structures
المؤلف:
........
المصدر:
LibreTexts Project
الجزء والصفحة:
............
24-4-2019
6082
Hexagonal Close-Packed and Cubic Close-Packed Structures
The most efficient way to pack spheres is the close-packed arrangement, which has two variants. A single layer of close-packed spheres is shown in part (a) in Figure 1.1 . Each sphere is surrounded by six others in the same plane to produce a hexagonal arrangement. Above any set of seven spheres are six depressions arranged in a hexagon. In principle, all six sites are the same, and any one of them could be occupied by an atom in the next layer. Actually, however, these six sites can be divided into two sets, labeled B and C in part (a) in Figure 1.1. Sites B and C differ because as soon as we place a sphere at a B position, we can no longer place a sphere in any of the three C positions adjacent to A and vice versa.
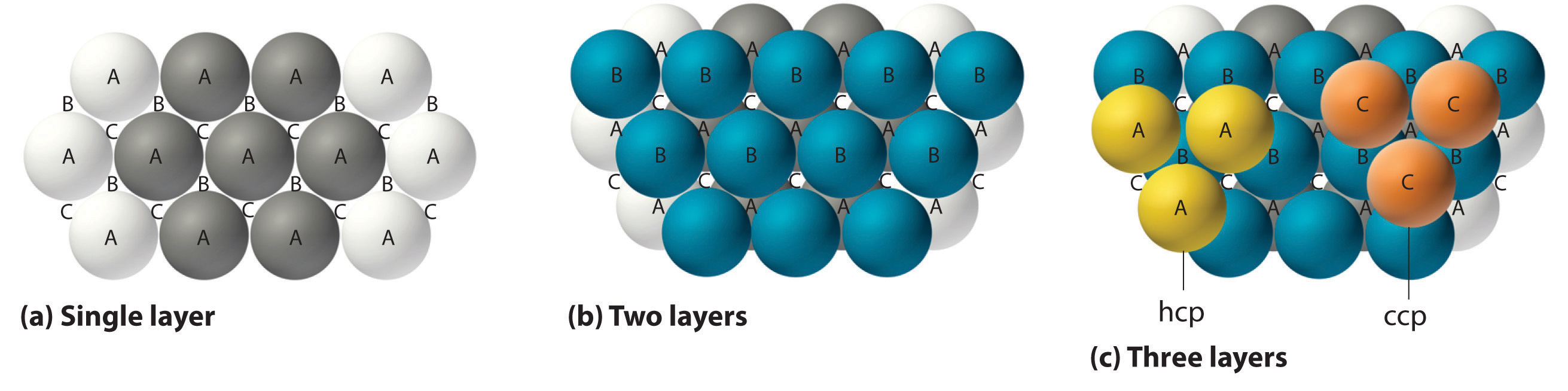
Figure 1.1 Close-Packed Layers of Spheres (a) In this single layer of close-packed spheres, each sphere is surrounded by six others in a hexagonal arrangement. (b) Placing an atom at a B position prohibits placing an atom at any of the adjacent C positions and results in all the atoms in the second layer occupying the B positions. (c) Placing the atoms in the third layer over the atoms at A positions in the first layer gives the hexagonal close-packed structure. Placing the third-layer atoms over the C positions gives the cubic close-packed structure.
If we place the second layer of spheres at the B positions in part (a) in Figure 1.1, we obtain the two-layered structure shown in part (b) in Figure 1.1. There are now two alternatives for placing the first atom of the third layer: we can place it directly over one of the atoms in the first layer (an A position) or at one of the C positions, corresponding to the positions that we did not use for the atoms in the first or second layers (part (c) in Figure 1.1 ). If we choose the first arrangement and repeat the pattern in succeeding layers, the positions of the atoms alternate from layer to layer in the pattern ABABAB…, resulting in a hexagonal close-packed (hcp) structureOne of two variants of the close-packed arrangement—the most efficient way to pack spheres in a lattice—in which the atomic positions alternate from layer to layer in an ABABAB… pattern. (part (a) in Figure 1.2). If we choose the second arrangement and repeat the pattern indefinitely, the positions of the atoms alternate as ABCABC…, giving a cubic close-packed (ccp) structureOne of two variants of the close-packed arrangement—the most efficient way to pack spheres in a lattice—in which the atomic positions alter from layer to layer in an ABCABC… pattern. (part (b) in Figure 1.2). Because the ccp structure contains hexagonally packed layers, it does not look particularly cubic. As shown in part (b) in Figure 1.2, however, simply rotating the structure reveals its cubic nature, which is identical to a fcc structure. The hcp and ccp structures differ only in the way their layers are stacked. Both structures have an overall packing efficiency of 74%, and in both each atom has 12 nearest neighbors (6 in the same plane plus 3 in each of the planes immediately above and below).

Figure 1.2 Close-Packed Structures: hcp and ccp The illustrations in (a) show an exploded view, a side view, and a top view of the hcp structure. The simple hexagonal unit cell is outlined in the side and top views. Note the similarity to the hexagonal unit cell . The ccp structure in (b) is shown in an exploded view, a side view, and a rotated view. The rotated view emphasizes the fcc nature of the unit cell (outlined). The line that connects the atoms in the first and fourth layers of the ccp structure is the body diagonal of the cube.
Table 1.1 compares the packing efficiency and the number of nearest neighbors for the different cubic and close-packed structures; the number of nearest neighbors is called the coordination numberThe number of nearest neighbors in a solid structure.. Most metals have hcp, ccp, or bcc structures, although several metals exhibit both hcp and ccp structures, depending on temperature and pressure.
Table 1.1 Properties of the Common Structures of Metals
| Structure | Percentage of Space Occupied by Atoms | Coordination Number |
|---|---|---|
| simple cubic | 52 | 6 |
| body-centered cubic | 68 | 8 |
| hexagonal close packed | 74 | 12 |
| cubic close packed (identical to face-centered cubic) | 74 | 12 |
 الاكثر قراءة في مقالات متنوعة في علم الكيمياء
الاكثر قراءة في مقالات متنوعة في علم الكيمياء
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















