Jacobi's Imaginary Transformation

Jacobi's imaginary transformations relate elliptic functions to other elliptic functions of the same type but having different arguments. In the case of the Jacobi elliptic functions 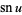, , 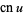and 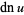, the transformations are

			(1)
			(2)
			(3)

where 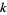 is the elliptic modulus, and  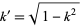is the complementary modulus (Abramowitz and Stegun 1972; Whittaker and Watson 1990, p. 505).

In the case of the Jacobi theta functions, Jacobi's imaginary transformation gives

			(4)
			(5)
			(6)
			(7)

where

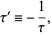(8)

and 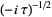 is interpreted as satisfying  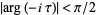(Whittaker and Watson 1990, p. 475).

Equation (6) can be written as the functional equation

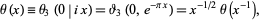(9)

where 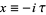 and  is the half-period ratio (Davenport 1980, p. 62). This form is useful for computing 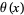 for small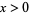, since then the series for  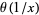converges much faster than that for 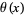. In his paper of 1859, Riemann used this functional equation for the theta function in one of his proofs of the functional equation for the Riemann zeta function (Davenport 1980).

These transformations were first obtained by Jacobi (1828), but Poisson (1827) had previously obtained a formula equivalent to one of the four, and from which the other three follow from elementary algebra (Whittaker and Watson 1990, p. 475)

REFERENCES:

Abramowitz, M. and Stegun, I. A. (Eds.). Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 592 and 595, 1972.

Borwein, J. M. and Borwein, P. B. Pi & the AGM: A Study in Analytic Number Theory and Computational Complexity. New York: Wiley, p. 73, 1987.

Davenport, H. Multiplicative Number Theory, 2nd ed. New York: Springer-Verlag, 1980.

Jacobi, C. G. J. "Suite des notices sur les fonctions elliptiques." J. reine angew. Math. 3, 403-404, 1828. Reprinted in Gesammelte Werke, Vol. 1. Providence, RI: Amer. Math. Soc., pp. 264-265, 1969.

Landsberg, G. "Zur Theorie der Gaussschen Summen und der linearen Transformation der Thetafunctionen." J. reine angew. Math. 111, 234-253, 1893.

Poisson, S. Mém. de l'Acad. des Sci. 6, 592, 1827.

Riemann, G. F. B. "Über die Anzahl der Primzahlen unter einer gegebenen Grösse." Monatsber. Königl. Preuss. Akad. Wiss. Berlin, 671-680, Nov. 1859.

Reprinted in Das Kontinuum und Andere Monographen (Ed. H. Weyl). New York: Chelsea, 1972.

Whittaker, E. T. and Watson, G. N. "Jacobi's Imaginary Transformation." §21.51 in A Course in Modern Analysis, 4th ed.Cambridge, England: Cambridge University Press, pp. 474-476 and 505, 1990.