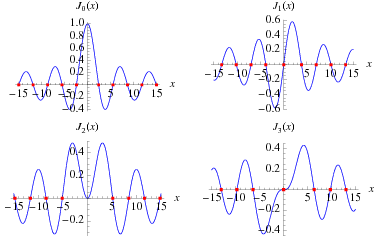
When the index  is real, the functions 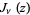, , 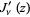, 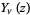and 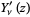 each have an infinite number of real zeros, all of which are simple with the possible exception of 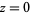. For nonnegative , the 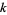th positive zeros of these functions are denote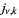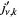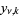d , , , and 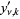, respectively, except that  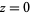is typically counted as the first zero of 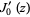(Abramowitz and Stegun 1972, p. 370).

The first few roots 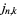 of the Bessel function  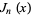are given in the following table for small nonnegative integer values of  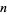and 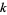. They can be found in the Wolfram Language using the command BesselJZero[n, k].

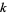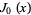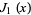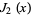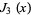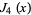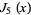1	2.4048	3.8317	5.1356	6.3802	7.5883	8.7715
2	5.5201	7.0156	8.4172	9.7610	11.0647	12.3386
3	8.6537	10.1735	11.6198	13.0152	14.3725	15.7002
4	11.7915	13.3237	14.7960	16.2235	17.6160	18.9801
5	14.9309	16.4706	17.9598	19.4094	20.8269	22.2178

The first few roots 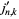 of the derivative of the Bessel function  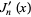are given in the following table for small nonnegative integer values of  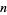and 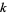. Versions of the Wolfram Language prior to 6 implemented these zeros as BesselJPrimeZeros[n, k] in the BesselZeros package which is now available for separate download (Wolfram Research). Note that contrary to Abramowitz and Stegun (1972, p. 370), the Wolfram Language defines the first zero of  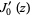to be approximately 3.8317 rather than zero.

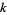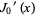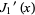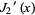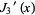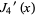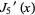1	3.8317	1.8412	3.0542	4.2012	5.3175	6.4156
2	7.0156	5.3314	6.7061	8.0152	9.2824	10.5199
3	10.1735	8.5363	9.9695	11.3459	12.6819	13.9872
4	13.3237	11.7060	13.1704	14.5858	15.9641	17.3128
5	16.4706	14.8636	16.3475	17.7887	19.1960	20.5755

REFERENCES:

Abramowitz, M. and Stegun, I. A. (Eds.). "Zeros." §9.5 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 370-374, 1972.

Goodwin, E. T. and Staton, J. "Table of 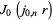." Quart. J. Mech. Appl. Math. 1, 220-224, 1948.

Olver, F. W. J. (Ed.). "Zeros and Associated Values." Royal Society Mathematical Tables, Vol. 7: Bessel Functions. Cambridge, England: Cambridge University Press, 1960.

Wolfram Research. "Wolfram Language & System Documentation Center: Upgrading from NumericalMath BesselZeros." http://reference.wolfram.com/language/Compatibility/tutorial/NumericalMath/BesselZeros.html.

Wolfram Research. "Wolfram Library Archive: NumericalMath BesselZeros Legacy Standard Add-On Package." library.wolfram.com/infocenter/MathSource/6777.

اخر الاخبار

اخبار العتبة العباسية المقدسة

قسم الشؤون الفكرية يقيم أمسيات قرآنية في غانا ونيجيريا ضمن برنامج سفرة الكفيل الرمضانية

شعبة التوجيه الديني النسوي تختتم محافلها القرآنية الرمضانية

المجمع العلمي يختتم مسابقة رحيق الولاء ضمن فعاليات ملتقى النورين الخامس في بابل

الحلقة 27 من جائزة العميد القرآنية تشهد مشاركة 5 قرّاء من فئة الكبار ضمن المرحلة النهائية

المزيد

الآخبار الصحية

كوب قبل النوم.. مشروب طبيعي يحارب الأرق

دون أدوية.. طريقة طبيعية لخفض ضغط الدم بفعالية مذهلة

المعكرونة ليست عدوك.. كيف تصبح جزءا من وجبة صحية متوازنة؟

دراسة: تناول القهوة يوميا يخفض خطر الإصابة بالاضطرابات النفسية

المزيد

الآخبار التكنلوجية

علماء روس يخططون لبناء منشأة للكشف عن المادة المظلمة

ثاني أكسيد الكربون ليس تهديدا للمناخ فقط.. بل لصحة الإنسان أيضا!

ديدان الأرض تكشف تلوث التربة بالمعادن الثقيلة

خبير أرصاد جوية: ظاهرة النينيو القادمة قد تكون الأقوى خلال 10 سنوات

المزيد