Polynomial Order
المؤلف:
Lidl, R. and Niederreiter, H.
المصدر:
Introduction to Finite Fields and their Applications, 2nd ed. New York: Cambridge University Press, 1994.
الجزء والصفحة:
...
13-2-2019
1114
Polynomial Order
The highest order power in a univariate polynomial is known as its order (or, more properly, its polynomial degree). For example, the polynomial
is of order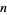 
, denoted 
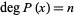. The order of a polynomial is implemented in the Wolfram Language as Exponent[poly, x].
It is preferable to use the word "degree" for the highest exponent in a polynomial, since a completely different meaning is given to the word "order" in polynomials taken modulo some integer (where this meaning is the one used in themultiplicative order of a modulus). In particular, the order of a polynomial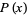 
with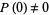 
is the smallest integer 
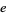for which 
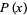divides 
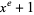(Lidl and Niederreiter 1994). For example, in the finite field GF(2), the order of 
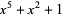is 31, since
This concept is closely related to that of the multiplicative order.
If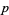 
is an irreducible polynomial of degree 
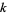, then its order has to divide the order of the multiplicative group in the corresponding field extension, i.e., 
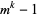for modulus 
.
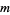REFERENCES:
Lidl, R. and Niederreiter, H. Introduction to Finite Fields and their Applications, 2nd ed. New York: Cambridge University Press, 1994.
الاكثر قراءة في مواضيع عامة في الجبر
اخر الاخبار
اخبار العتبة العباسية المقدسة
