Polynomial Discriminant

A polynomial discriminant is the product of the squares of the differences of the polynomial roots 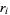. The discriminant of a polynomial is defined only up to constant factor, and several slightly different normalizations can be used. For a polynomial

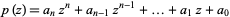(1)

of degree 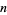, the most common definition of the discriminant is

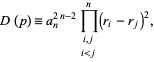(2)

which gives a homogenous polynomial of degree 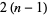 in the coefficients of .

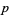The discriminant of a polynomial 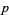 is given in terms of a resultant as

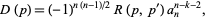(3)

where 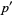 is the derivative of  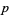and 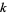 is the degree of 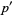. For fields of infinite characteristic,  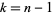so the formula reduces to

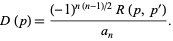(4)

The discriminant of a univariate polynomial 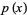 is implemented in the Wolfram Language as Discriminant[p, x].

The discriminant of the quadratic equation

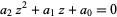(5)

is given by

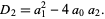(6)

The discriminant of the cubic equation

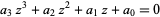(7)

is given by

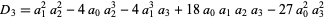(8)

The discriminant of a quartic equation

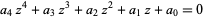(9)

is

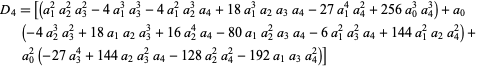(10)

(Schroeppel 1972).

REFERENCES:

Akritas, A. G. Elements of Computer Algebra with Applications. New York: Wiley, 1989.

Basu, S.; Pollack, R.; and Roy, M.-F. Algorithms in Real Algebraic Geometry. Berlin: Springer-Verlag, 2003.

Caviness, B. F. and Johnson, J. R. (Eds.). Quantifier Elimination and Cylindrical Algebraic Decomposition. New York: Springer-Verlag, 1998.

Cohen, H. "Resultants and Discriminants." §3.3.2 in A Course in Computational Algebraic Number Theory. New York: Springer-Verlag, pp. 119-123, 1993.

Cox, D.; Little, J.; and O'Shea, D. Ideals, Varieties, and Algorithms: An Introduction to Algebraic Geometry and Commutative Algebra, 2nd ed. New York: Springer-Verlag, 1996.

Mignotte, M. and Stefănescu, D. Polynomials: An Algorithmic Approach. Singapore: Springer-Verlag, 1999.

Schroeppel, R. Item 4 in Beeler, M.; Gosper, R. W.; and Schroeppel, R. HAKMEM. Cambridge, MA: MIT Artificial Intelligence Laboratory, Memo AIM-239, p. 4, Feb. 1972. http://www.inwap.com/pdp10/hbaker/hakmem/geometry.html#item4.

Zippel, R. Effective Polynomial Computation. Boston, MA: Kluwer, 1993.