
 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 28-10-2018
Date: 25-11-2018
Date: 26-12-2018
|
If 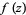 is continuous in a region
is continuous in a region 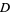 and satisfies
and satisfies
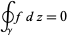 |
for all closed contours 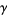 in
in 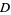 , then
, then 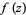 is analytic in
is analytic in 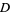 .
.
Morera's theorem does not require simple connectedness, which can be seen from the following proof. Let 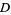 be a region, with
be a region, with 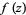 continuous on
continuous on 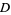 , and let its integrals around closed loops be zero. Pick any point
, and let its integrals around closed loops be zero. Pick any point 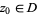 , and pick a neighborhood of
, and pick a neighborhood of 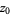 . Construct an integral of
. Construct an integral of 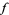 ,
,
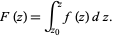 |
Then one can show that 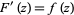 , and hence
, and hence 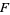 is analytic and has derivatives of all orders, as does
is analytic and has derivatives of all orders, as does 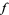 , so
, so 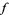 is analytic at
is analytic at 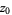 . This is true for arbitrary
. This is true for arbitrary 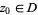 , so
, so 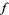 is analytic in
is analytic in 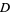 .
.
It is, in fact, sufficient to require that the integrals of 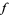 around triangles be zero, but this is a technical point. In this case, the proof is identical except
around triangles be zero, but this is a technical point. In this case, the proof is identical except 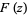 must be constructed by integrating along the line segment
must be constructed by integrating along the line segment 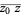 instead of along an arbitrary path.
instead of along an arbitrary path.
REFERENCES:
Arfken, G. Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 373-374, 1985.
Krantz, S. G. Handbook of Complex Variables. Boston, MA: Birkhäuser, p. 26, 1999.



|
|
|
|
للعاملين في الليل.. حيلة صحية تجنبكم خطر هذا النوع من العمل
|
|
|
|
|
|
|
"ناسا" تحتفي برائد الفضاء السوفياتي يوري غاغارين
|
|
|
|
|
|
|
ملاكات العتبة العباسية المقدسة تُنهي أعمال غسل حرم مرقد أبي الفضل العباس (عليه السلام) وفرشه
|
|
|