

تاريخ الرياضيات

الاعداد و نظريتها

تاريخ التحليل

تار يخ الجبر

الهندسة و التبلوجي


الرياضيات في الحضارات المختلفة

العربية

اليونانية

البابلية

الصينية

المايا

المصرية

الهندية


الرياضيات المتقطعة

المنطق

اسس الرياضيات

فلسفة الرياضيات

مواضيع عامة في المنطق


الجبر

الجبر الخطي

الجبر المجرد

الجبر البولياني

مواضيع عامة في الجبر

الضبابية

نظرية المجموعات

نظرية الزمر

نظرية الحلقات والحقول

نظرية الاعداد

نظرية الفئات

حساب المتجهات

المتتاليات-المتسلسلات

المصفوفات و نظريتها

المثلثات


الهندسة

الهندسة المستوية

الهندسة غير المستوية

مواضيع عامة في الهندسة

التفاضل و التكامل


المعادلات التفاضلية و التكاملية

معادلات تفاضلية

معادلات تكاملية

مواضيع عامة في المعادلات


التحليل

التحليل العددي

التحليل العقدي

التحليل الدالي

مواضيع عامة في التحليل

التحليل الحقيقي

التبلوجيا

نظرية الالعاب

الاحتمالات و الاحصاء

نظرية التحكم

بحوث العمليات

نظرية الكم

الشفرات

الرياضيات التطبيقية

نظريات ومبرهنات


علماء الرياضيات

500AD

500-1499

1000to1499

1500to1599

1600to1649

1650to1699

1700to1749

1750to1779

1780to1799

1800to1819

1820to1829

1830to1839

1840to1849

1850to1859

1860to1864

1865to1869

1870to1874

1875to1879

1880to1884

1885to1889

1890to1894

1895to1899

1900to1904

1905to1909

1910to1914

1915to1919

1920to1924

1925to1929

1930to1939

1940to the present

علماء الرياضيات

الرياضيات في العلوم الاخرى

بحوث و اطاريح جامعية

هل تعلم

طرائق التدريس

الرياضيات العامة

نظرية البيان
Tautochrone Problem
المؤلف:
Gardner, M.
المصدر:
The Sixth Book of Mathematical Games from Scientific American. Chicago, IL: University of Chicago Press
الجزء والصفحة:
...
12-10-2018
2211
Tautochrone Problem
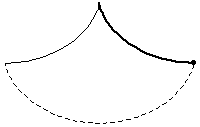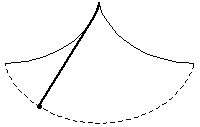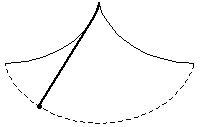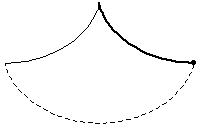
The problem of finding the curve down which a bead placed anywhere will fall to the bottom in the same amount of time. The solution is a cycloid, a fact first discovered and published by Huygens in Horologium oscillatorium (1673). This property was also alluded to in the following passage from Moby Dick: "[The try-pot] is also a place for profound mathematical meditation. It was in the left-hand try-pot of the Pequod, with the soapstone diligently circling round me, that I was first indirectly struck by the remarkable fact, that in geometry all bodies gliding along a cycloid, my soapstone, for example, will descend from any point in precisely the same time" (Melville 1851).
Huygens also constructed the first pendulum clock with a device to ensure that the pendulum was isochronous by forcing the pendulum to swing in an arc of a cycloid. This is accomplished by placing two evolutes of inverted cycloid arcs on each side of the pendulum's point of suspension against which the pendulum is constrained to move (Wells 1991, p. 47; Gray 1997, p. 123). Unfortunately, friction along the arcs causes a greater error than that corrected by the cycloidal path (Gardner 1984).
The parametric equations of the cycloid are
 |
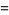 |
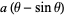 |
(1) |
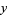 |
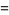 |
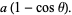 |
(2) |
To see that the cycloid satisfies the tautochrone property, consider the derivatives
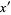 |
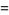 |
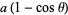 |
(3) |
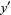 |
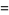 |
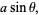 |
(4) |
and
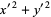 |
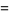 |
![a^2[(1-2costheta+cos^2theta)+sin^2theta]](http://mathworld.wolfram.com/images/equations/TautochroneProblem/Inline15.gif) |
(5) |
 |
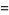 |
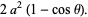 |
(6) |
Now
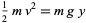 |
(7) |
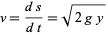 |
(8) |
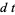 |
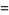 |
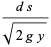 |
(9) |
 |
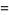 |
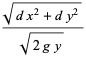 |
(10) |
 |
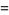 |
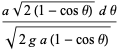 |
(11) |
 |
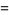 |
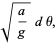 |
(12) |
so the time required to travel from the top of the cycloid to the bottom is
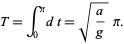 |
(13) |
However, from an intermediate point 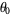 ,
,
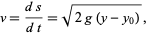 |
(14) |
so
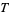 |
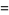 |
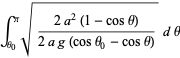 |
(15) |
 |
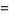 |
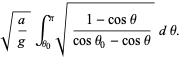 |
(16) |
To integrate, rearrange this equation using the half-angle formulas
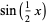 |
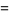 |
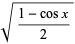 |
(17) |
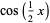 |
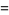 |
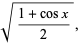 |
(18) |
with the latter rewritten in the form
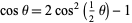 |
(19) |
to obtain
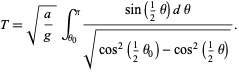 |
(20) |
Now transform variables to
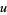 |
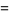 |
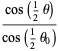 |
(21) |
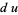 |
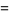 |
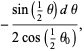 |
(22) |
so
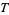 |
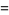 |
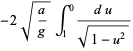 |
(23) |
 |
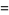 |
![2sqrt(a/g)[sin^(-1)u]_0^1](http://mathworld.wolfram.com/images/equations/TautochroneProblem/Inline55.gif) |
(24) |
 |
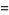 |
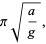 |
(25) |
and the amount of time is the same from any point.
REFERENCES:
Gardner, M. The Sixth Book of Mathematical Games from Scientific American. Chicago, IL: University of Chicago Press, pp. 129-130, 1984.
Gray, A. Modern Differential Geometry of Curves and Surfaces with Mathematica, 2nd ed. Boca Raton, FL: CRC Press, 1997.
Lagrange, J. L. "Sue les courbes tautochrones." Mém. de l'Acad. Roy. des Sci. et Belles-Lettres de Berlin 21, 1765. Reprinted in Oeuvres de Lagrange, tome 2, section deuxième: Mémoires extraits des recueils de l'Academie royale des sciences et Belles-Lettres de Berlin. Paris: Gauthier-Villars, pp. 317-332, 1868.
Melville, H. "The Tryworks." Ch. 96 in Moby Dick. New York: Bantam, 1981. Originally published in 1851.
Muterspaugh, J.; Driver, T.; and Dick, J. E. "The Cycloid and Tautochronism." http://php.indiana.edu/~jedick/project/intro.html
Muterspaugh, J.; Driver, T.; and Dick, J. E. "P221 Tautochrone Problem." http://php.indiana.edu/~jedick/project/project.html
Phillips, J. P. "Brachistochrone, Tautochrone, Cycloid--Apple of Discord." Math. Teacher 60, 506-508, 1967.
Wagon, S. Mathematica in Action. New York: W. H. Freeman, pp. 54-60 and 384-385, 1991.
Wells, D. The Penguin Dictionary of Curious and Interesting Geometry. London: Penguin, pp. 46-47, 1991.
 الاكثر قراءة في التفاضل و التكامل
الاكثر قراءة في التفاضل و التكامل
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















