

تاريخ الرياضيات

الاعداد و نظريتها

تاريخ التحليل

تار يخ الجبر

الهندسة و التبلوجي


الرياضيات في الحضارات المختلفة

العربية

اليونانية

البابلية

الصينية

المايا

المصرية

الهندية


الرياضيات المتقطعة

المنطق

اسس الرياضيات

فلسفة الرياضيات

مواضيع عامة في المنطق


الجبر

الجبر الخطي

الجبر المجرد

الجبر البولياني

مواضيع عامة في الجبر

الضبابية

نظرية المجموعات

نظرية الزمر

نظرية الحلقات والحقول

نظرية الاعداد

نظرية الفئات

حساب المتجهات

المتتاليات-المتسلسلات

المصفوفات و نظريتها

المثلثات


الهندسة

الهندسة المستوية

الهندسة غير المستوية

مواضيع عامة في الهندسة

التفاضل و التكامل


المعادلات التفاضلية و التكاملية

معادلات تفاضلية

معادلات تكاملية

مواضيع عامة في المعادلات


التحليل

التحليل العددي

التحليل العقدي

التحليل الدالي

مواضيع عامة في التحليل

التحليل الحقيقي

التبلوجيا

نظرية الالعاب

الاحتمالات و الاحصاء

نظرية التحكم

بحوث العمليات

نظرية الكم

الشفرات

الرياضيات التطبيقية

نظريات ومبرهنات


علماء الرياضيات

500AD

500-1499

1000to1499

1500to1599

1600to1649

1650to1699

1700to1749

1750to1779

1780to1799

1800to1819

1820to1829

1830to1839

1840to1849

1850to1859

1860to1864

1865to1869

1870to1874

1875to1879

1880to1884

1885to1889

1890to1894

1895to1899

1900to1904

1905to1909

1910to1914

1915to1919

1920to1924

1925to1929

1930to1939

1940to the present

علماء الرياضيات

الرياضيات في العلوم الاخرى

بحوث و اطاريح جامعية

هل تعلم

طرائق التدريس

الرياضيات العامة

نظرية البيان
Brachistochrone Problem
المؤلف:
Ashby, N.; Brittin, W. E.; Love, W. F.; and Wyss, W.
المصدر:
"Brachistochrone with Coulomb Friction." Amer. J. Phys. 43
الجزء والصفحة:
...
12-10-2018
4086
Brachistochrone Problem
Find the shape of the curve down which a bead sliding from rest and accelerated by gravity will slip (without friction) from one point to another in the least time. The term derives from the Greek 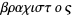 (brachistos) "the shortest" and
(brachistos) "the shortest" and 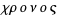 (chronos) "time, delay."
(chronos) "time, delay."
The brachistochrone problem was one of the earliest problems posed in the calculus of variations. Newton was challenged to solve the problem in 1696, and did so the very next day (Boyer and Merzbach 1991, p. 405). In fact, the solution, which is a segment of a cycloid, was found by Leibniz, L'Hospital, Newton, and the two Bernoullis. Johann Bernoulli solved the problem using the analogous one of considering the path of light refracted by transparent layers of varying density (Mach 1893, Gardner 1984, Courant and Robbins 1996). Actually, Johann Bernoulli had originally found an incorrect proof that the curve is a cycloid, and challenged his brother Jakob to find the required curve. When Jakob correctly did so, Johann tried to substitute the proof for his own (Boyer and Merzbach 1991, p. 417).
In the solution, the bead may actually travel uphill along the cycloid for a distance, but the path is nonetheless faster than a straight line (or any other line).
The time to travel from a point 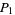 to another point
to another point 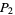 is given by the integral
is given by the integral
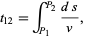 |
(1) |
where 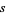 is the arc length and
is the arc length and 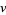 is the speed. The speed at any point is given by a simple application of conservation of energy equating kinetic energy to gravitational potential energy,
is the speed. The speed at any point is given by a simple application of conservation of energy equating kinetic energy to gravitational potential energy,
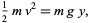 |
(2) |
giving
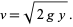 |
(3) |
Plugging this into (◇) together with the identity
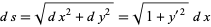 |
(4) |
then gives
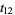 |
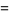 |
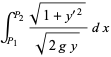 |
(5) |
 |
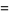 |
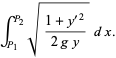 |
(6) |
The function to be varied is thus
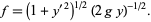 |
(7) |
To proceed, one would normally have to apply the full-blown Euler-Lagrange differential equation
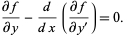 |
(8) |
However, the function 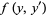 is particularly nice since
is particularly nice since  does not appear explicitly. Therefore,
does not appear explicitly. Therefore, 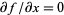 , and we can immediately use the Beltrami identity
, and we can immediately use the Beltrami identity
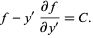 |
(9) |
Computing
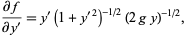 |
(10) |
subtracting 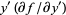 from
from 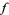 , and simplifying then gives
, and simplifying then gives
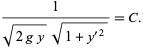 |
(11) |
Squaring both sides and rearranging slightly results in
![[1+((dy)/(dx))^2]y](http://mathworld.wolfram.com/images/equations/BrachistochroneProblem/Inline18.gif) |
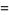 |
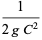 |
(12) |
 |
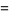 |
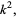 |
(13) |
where the square of the old constant 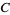 has been expressed in terms of a new (positive) constant
has been expressed in terms of a new (positive) constant 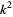 . This equation is solved by the parametric equations
. This equation is solved by the parametric equations
 |
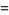 |
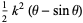 |
(14) |
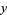 |
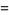 |
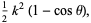 |
(15) |
which are--lo and behold--the equations of a cycloid.
If kinetic friction is included, the problem can also be solved analytically, although the solution is significantly messier. In that case, terms corresponding to the normal component of weight and the normal component of the acceleration(present because of path curvature) must be included. Including both terms requires a constrained variational technique (Ashby et al. 1975), but including the normal component of weight only gives an approximate solution. The tangent and normal vectors are
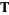 |
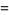 |
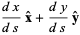 |
(16) |
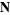 |
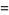 |
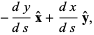 |
(17) |
gravity and friction are then
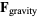 |
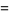 |
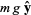 |
(18) |
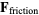 |
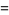 |
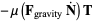 |
(19) |
 |
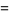 |
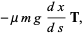 |
(20) |
and the components along the curve are
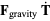 |
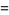 |
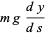 |
(21) |
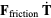 |
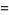 |
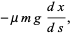 |
(22) |
so Newton's Second Law gives
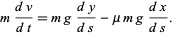 |
(23) |
But
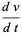 |
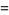 |
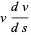 |
(24) |
 |
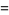 |
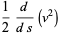 |
(25) |
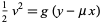 |
(26) |
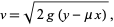 |
(27) |
so
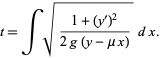 |
(28) |
Using the Euler-Lagrange differential equation gives
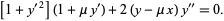 |
(29) |
This can be reduced to
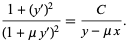 |
(30) |
Now letting
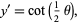 |
(31) |
the solution is
 |
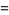 |
![1/2k^2[(theta-sintheta)+mu(1-costheta)]](http://mathworld.wolfram.com/images/equations/BrachistochroneProblem/Inline61.gif) |
(32) |
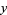 |
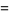 |
![1/2k^2[(1-costheta)+mu(theta+sintheta)].](http://mathworld.wolfram.com/images/equations/BrachistochroneProblem/Inline64.gif) |
(33) |
REFERENCES:
Ashby, N.; Brittin, W. E.; Love, W. F.; and Wyss, W. "Brachistochrone with Coulomb Friction." Amer. J. Phys. 43, 902-905, 1975.
Boyer, C. B. and Merzbach, U. C. A History of Mathematics, 2nd ed. New York: Wiley, 1991.
Courant, R. and Robbins, H. What Is Mathematics?: An Elementary Approach to Ideas and Methods, 2nd ed. Oxford, England: Oxford University Press, 1996.
Gardner, M. The Sixth Book of Mathematical Games from Scientific American. Chicago, IL: University of Chicago Press, pp. 130-131, 1984.
Haws, L. and Kiser, T. "Exploring the Brachistochrone Problem." Amer. Math. Monthly 102, 328-336, 1995.
Hayen, J. C. "Brachistochrone with Coulomb Friction." Int. J. Non-Linear Mech. 40, 1057-1075, 2005.
Lipp, S. C. "Brachistochrone with Coulomb Friction." SIAM J. Control Optim. 35, 562-584, 1997.
Mach, E. The Science of Mechanics. Chicago, IL: Open Court, 1893.
Phillips, J. P. "Brachistochrone, Tautochrone, Cycloid--Apple of Discord." Math. Teacher 60, 506-508, 1967.
Smith, D. E. History of Mathematics, Vol. 2: Special Topics of Elementary Mathematics. New York: Dover, p. 326, 1958.
Steinhaus, H. Mathematical Snapshots, 3rd ed. New York: Dover, pp. 148-149, 1999.
Wagon, S. Mathematica in Action. New York: W. H. Freeman, pp. 60-66 and 385-389, 1991.
Wells, D. The Penguin Dictionary of Curious and Interesting Geometry. London: Penguin, p. 46, 1991.
 الاكثر قراءة في التفاضل و التكامل
الاكثر قراءة في التفاضل و التكامل
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















