Limit
The term limit comes about relative to a number of topics from several different branches of mathematics.
A sequence 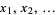 of elements in a topological space
of elements in a topological space 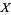 is said to have limit
is said to have limit  provided that for each neighborhood
provided that for each neighborhood 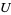 of
of  , there exists a natural number
, there exists a natural number 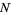 so that
so that 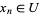 for all
for all 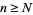 . This very general definition can be specialized in the event that
. This very general definition can be specialized in the event that 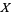 is a metric space, whence one says that a sequence
is a metric space, whence one says that a sequence ![<span style=]() {x_n}" src="http://mathworld.wolfram.com/images/equations/Limit/Inline10.gif" style="height:14px; width:23px" /> in
{x_n}" src="http://mathworld.wolfram.com/images/equations/Limit/Inline10.gif" style="height:14px; width:23px" /> in 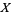 has limit
has limit 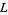 if for all
if for all 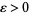 , there exists a natural number
, there exists a natural number 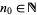 so that
so that
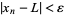 |
(1)
|
for all 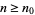 . In many commonly-encountered scenarios, limits are unique, whereby one says that
. In many commonly-encountered scenarios, limits are unique, whereby one says that 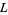 is the limit of
is the limit of ![<span style=]() {x_n}" src="http://mathworld.wolfram.com/images/equations/Limit/Inline17.gif" style="height:14px; width:23px" /> and writes
{x_n}" src="http://mathworld.wolfram.com/images/equations/Limit/Inline17.gif" style="height:14px; width:23px" /> and writes
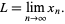 |
(2)
|
On the other hand, a sequence of elements from an metric space 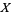 may have several - even infinitely many - different limits provided that
may have several - even infinitely many - different limits provided that 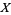 is equipped with a topology which fails to be T2. One reads the expression in (1) as "the limit as
is equipped with a topology which fails to be T2. One reads the expression in (1) as "the limit as 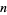 approaches infinity of
approaches infinity of 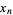 is
is 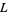 ."
."
The topological notion of convergence can be rewritten to accommodate a wider array of topological spaces 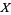 by utilizing the language of nets. In particular, if
by utilizing the language of nets. In particular, if ![x=<span style=]() {x_i}" src="http://mathworld.wolfram.com/images/equations/Limit/Inline24.gif" style="height:14px; width:45px" /> is a net from a directed set
{x_i}" src="http://mathworld.wolfram.com/images/equations/Limit/Inline24.gif" style="height:14px; width:45px" /> is a net from a directed set 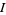 into
into 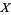 , then an element
, then an element 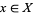 is said to be the limit of
is said to be the limit of  if and only if for every neighborhood
if and only if for every neighborhood 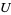 of
of  ,
,  is eventually in
is eventually in 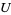 , i.e., if there exists an
, i.e., if there exists an 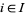 so that, for every
so that, for every 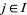 with
with 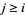 , the point
, the point 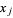 lies in
lies in 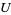 . This notion is particularly well-purposed for topological spaces which aren't first-countable.
. This notion is particularly well-purposed for topological spaces which aren't first-countable.
A function 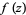 is said to have a finite limit
is said to have a finite limit 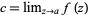 if, for all
if, for all 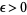 , there exists a
, there exists a 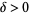 such that
such that 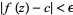 whenever
whenever 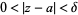 . This form of definition is sometimes called an epsilon-delta definition. This can be adapted to the case of infinite limits as well: The limit of
. This form of definition is sometimes called an epsilon-delta definition. This can be adapted to the case of infinite limits as well: The limit of 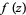 as
as 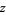 approaches
approaches 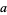 is equal to
is equal to 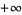 (respectively
(respectively 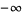 ) if for every number
) if for every number 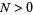 (respectively
(respectively 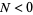 ), there exists a number
), there exists a number 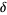 depending on
depending on 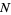 for which
for which 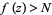 (respectively,
(respectively, 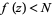 ) whenever
) whenever 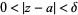 . Similar adjustments can be made to define limits of functions
. Similar adjustments can be made to define limits of functions 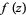 when
when 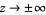 .
.
Limits may be taken from below
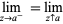 |
(3)
|
or from above
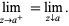 |
(4)
|
if the two are equal, then "the" limit is said to exist
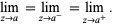 |
(5)
|
The expression in (2) is read "the limit as 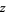 approaches
approaches 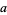 from the left / from below" or "the limit as
from the left / from below" or "the limit as 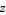 increases to
increases to 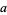 ," while (3) is read "the limit as
," while (3) is read "the limit as 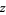 approaches
approaches 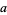 from the right / from above" or "the limit as
from the right / from above" or "the limit as 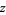 decreases to
decreases to 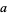 ." In (4), one simply refers to "the limit as
." In (4), one simply refers to "the limit as 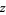 approaches
approaches 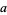 ."
."
Limits are implemented in the Wolfram Language as Limit[f, x-> x0]. This command also takes options Direction (which can be set to any complex direction, including for example 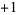 ,
, 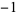 , I, and -I), and Analytic, which computes symbolic limits for functions.
, I, and -I), and Analytic, which computes symbolic limits for functions.
Note that the function definition of limit can be thought of as a natural generalization of the sequence definition due to the fact that a sequence 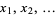 in a topological space
in a topological space 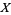 is nothing more than a function
is nothing more than a function 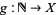 mapping
mapping 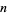 to
to 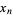 .
.
A lower limit 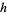
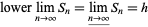 |
(6)
|
is said to exist if, for every 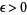 ,
, 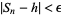 for infinitely many values of
for infinitely many values of 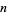 and if no number less than
and if no number less than 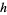 has this property.
has this property.
An upper limit 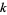
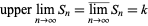 |
(7)
|
is said to exist if, for every 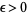 ,
, 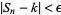 for infinitely many values of
for infinitely many values of 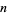 and if no number larger than
and if no number larger than 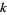 has this property.
has this property.
Related notions include supremum limit and infimum limit.
Indeterminate limit forms of types 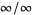 and
and 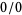 can often be computed with L'Hospital's rule. Types
can often be computed with L'Hospital's rule. Types 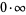 can be converted to the form
can be converted to the form 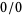 by writing
by writing
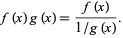 |
(8)
|
Types 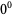 ,
, 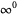 , and
, and 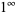 are treated by introducing a dependent variable
are treated by introducing a dependent variable
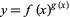 |
(9)
|
so that
![lny=g(x)ln[f(x)],](http://mathworld.wolfram.com/images/equations/Limit/NumberedEquation10.gif) |
(10)
|
then calculating lim 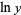 . The original limit then equals
. The original limit then equals 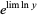 ,
,
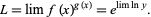 |
(11)
|
The indeterminate form 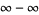 is also frequently encountered.
is also frequently encountered.
All of the above notions can be generalized even further by utilizing the language of ultrafilters. In particular, if 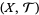 is a topological space and if
is a topological space and if 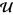 is an ultrafilter on
is an ultrafilter on 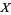 , then an element
, then an element 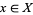 is said to be a limit of
is said to be a limit of 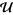 if every neighborhood of
if every neighborhood of  belongs to
belongs to 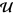 . Several authors have defined similar ideas relative to filters as well (Stadler and Stadler 2002).
. Several authors have defined similar ideas relative to filters as well (Stadler and Stadler 2002).
The June 2, 1996 comic strip FoxTrot by Bill Amend (Amend 1998, p. 19; Mitchell 2006/2007) featured the following limit as a "hard" exam problem intended for a remedial math class but accidentally handed out to the normal class:
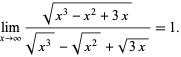 |
(12)
|

REFERENCES:
Amend, B. Camp FoxTrot. Kansas City, MO: Andrews McMeel, p. 19, 1998.
Clark, P. L. "Convergence." 2014. http://math.uga.edu/~pete/convergence.pdf.
Courant, R. and Robbins, H. "Limits. Infinite Geometrical Series." §2.2.3 in What Is Mathematics?: An Elementary Approach to Ideas and Methods, 2nd ed. Oxford, England: Oxford University Press, pp. 63-66, 1996.
Gruntz, D. On Computing Limits in a Symbolic Manipulation System. Doctoral thesis. Zürich: Swiss Federal Institute of Technology, 1996.
Hight, D. W. A Concept of Limits. New York: Prentice-Hall, 1966.
Kaplan, W. "Limits and Continuity." §2.4 in Advanced Calculus, 4th ed. Reading, MA: Addison-Wesley, pp. 82-86, 1992.
Miller, N. Limits: An Introductory Treatment. Waltham, MA: Blaisdell, 1964.
Mitchell, C. W. Jr. In "Media Clips" (Ed. M. Cibes and J. Greenwood). Math. Teacher 100, 339, Dec. 2006/Jan. 2007.
Munkres, J. Topology 2nd Edition. Upper Saddle River, NJ: Prentice Hall, Inc., 2000.
Nagy, G. "The Concept of Convergence: Ultrafilters and Nets." 2008. http://www.math.ksu.edu/~nagy/real-an/1-02-convergence.pdf.
Prevost, S. "Exploring the 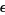 -
-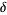 Definition of Limit with Mathematica." Mathematica Educ. 3, 17-21, 1994.
Definition of Limit with Mathematica." Mathematica Educ. 3, 17-21, 1994.
Smith, W. K. Limits and Continuity. New York: Macmillan, 1964.
Stadler, B. M. R. and Stadler, P. F. "Basic Properties of Filter Convergence Spaces." 2002. https://www.bioinf.uni-leipzig.de/~studla/Publications/PREPRINTS/01-pfs-007-subl1.pdf.
 الاكثر قراءة في التفاضل و التكامل
الاكثر قراءة في التفاضل و التكامل
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


