
Integration by Parts
 المؤلف:
Abramowitz, M. and Stegun, I. A.
المؤلف:
Abramowitz, M. and Stegun, I. A.
 المصدر:
Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing.New York: Dover
المصدر:
Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing.New York: Dover
 الجزء والصفحة:
...
الجزء والصفحة:
...
 17-9-2018
17-9-2018
 2861
2861
Integration by Parts
Integration by parts is a technique for performing indefinite integration 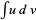 or definite integration
or definite integration 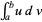 by expanding the differential of a product of functions
by expanding the differential of a product of functions 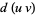 and expressing the original integral in terms of a known integral
and expressing the original integral in terms of a known integral 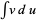 . A single integration by parts starts with
. A single integration by parts starts with
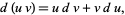 |
(1)
|
and integrates both sides,
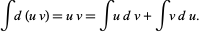 |
(2)
|
Rearranging gives
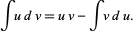 |
(3)
|
For example, consider the integral 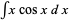 and let
and let
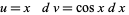 |
(4)
|
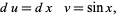 |
(5)
|
so integration by parts gives
where 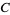 is a constant of integration.
is a constant of integration.
The procedure does not always succeed, since some choices of 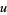 may lead to more complicated integrals than the original. For example, consider again the integral
may lead to more complicated integrals than the original. For example, consider again the integral 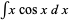 and let
and let
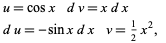 |
(8)
|
giving
which is more difficult than the original (Apostol 1967, pp. 218-219).
Integration by parts may also fail because it leads back to the original integral. For example, consider 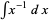 and let
and let
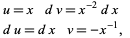 |
(11)
|
then
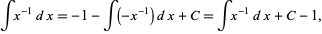 |
(12)
|
which is same integral as the original (Apostol 1967, p. 219).
The analogous procedure works for definite integration by parts, so
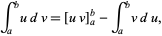 |
(13)
|
where 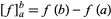 .
.
Integration by parts can also be applied 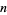 times to
times to 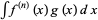 :
:
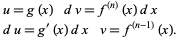 |
(14)
|
Therefore,
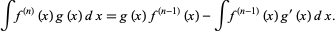 |
(15)
|
But
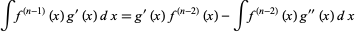 |
(16)
|
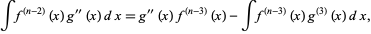 |
(17)
|
so
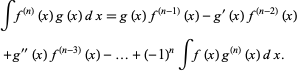 |
(18)
|
Now consider this in the slightly different form 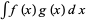 . Integrate by parts a first time
. Integrate by parts a first time
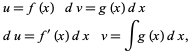 |
(19)
|
so
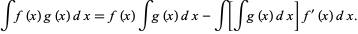 |
(20)
|
Now integrate by parts a second time,
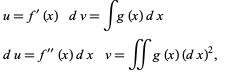 |
(21)
|
so
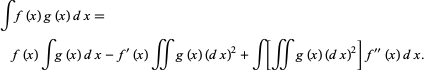 |
(22)
|
Repeating a third time,
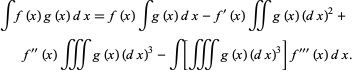 |
(23)
|
Therefore, after 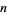 applications,
applications,
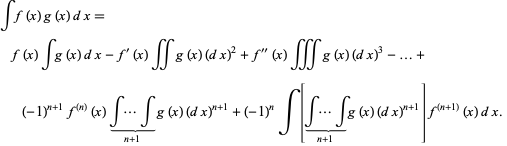 |
(24)
|
If 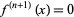 (e.g., for an
(e.g., for an 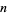 th degree polynomial), the last term is 0, so the sum terminates after
th degree polynomial), the last term is 0, so the sum terminates after 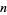 terms and
terms and
 |
(25)
|
REFERENCES:
Abramowitz, M. and Stegun, I. A. (Eds.). Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing.New York: Dover, p. 12, 1972.
Apostol, T. M. "Integration by Parts." §5.9 in Calculus, 2nd ed., Vol. 1: One-Variable Calculus, with an Introduction to Linear Algebra. Waltham, MA: Blaisdell, pp. 217-220, 1967.
Bronshtein, I. N. and Semendyayev, K. A. Handbook of Mathematics, 3rd ed. New York: Springer-Verlag, p. 269, 1997.
 الاكثر قراءة في التفاضل و التكامل
الاكثر قراءة في التفاضل و التكامل
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


