Watson,s Triple Integrals
المؤلف:
Bailey, D. H.; Borwein, J. M.; Kapoor, V.; and Weisstein, E. W
المصدر:
"Ten Problems in Experimental Mathematics." Amer. Math. Monthly 113
الجزء والصفحة:
...
17-9-2018
2277
Watson's Triple Integrals
Watson (1939) considered the following three triple integrals,
(OEIS A091670, A091671, and A091672), where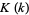 
is a complete elliptic integral of the first kind, 
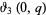is a Jacobi theta function, and 
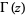is the gamma function. Analytic computation of these integrals is rather challenging, especially 
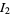and 
.
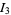Watson (1939) treats all three integrals by making the transformations
regarding 
, 
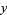, and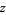 
as Cartesian coordinates, and changing to polar coordinates,
after writing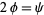 
.
Performing this transformation on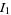 
gives
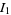can then be directly integrated using computer algebra, although Watson (1939) used the additional transformation
 |
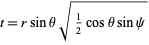(25)
|
to separate the integral into
The integral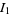 
can also be done by performing one of the integrations
 |
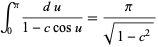(29)
|
with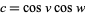 
to obtain
 |
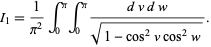(30)
|
Expanding using a binomial series
where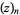 
is a Pochhammer symbol and
 |
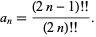(33)
|
Integrating gives
Now, as a result of the amazing identity for the complete elliptic integral of the first kind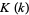 
 |
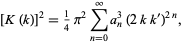(38)
|
where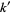 
is the complementary modulus and 
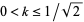(Watson 1908, Watson 1939), it follows immediately that with 
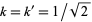(i.e., 
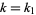, the first singular value),
 |
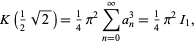(39)
|
so
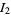can be transformed using the same prescription to give
where the substitution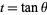 
has been made in the last step. Computer algebra can return this integral in the form of a Meijer G-function
 |
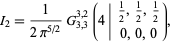(48)
|
but more clever treatment is needed to obtain it in a nicer form. For example, Watson (1939) notes that
 |
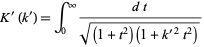(49)
|
immediately gives
 |
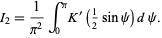(50)
|
However, quadrature of this integral requires very clever use of a complicated series identity for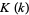 
to obtain term by term integration that can then be recombined as recognized as
 |
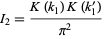(51)
|
(Watson 1939).
For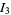 
, only a single integration can be done analytically, namely
 |
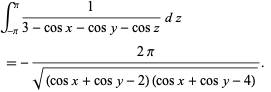(52)
|
It can be reduced to a single infinite sum by defining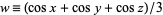 
and using a binomial series expansion to write
 |
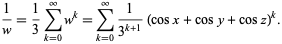(53)
|
But this can then be written as a multinomial series and plugged back in to obtain
 |
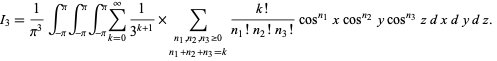(54)
|
Exchanging the order of integration and summation allows the integrals to be done, leading to
 |
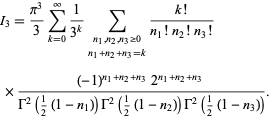(55)
|
Rather surprisingly, the sums over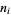 
can be done in closed form, yielding
 |
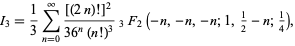(56)
|
where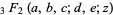 
is a generalized hypergeometric function. However, this sum cannot be done in closed form.
Watson (1939) transformed the integral to
 |
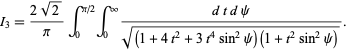(57)
|
However, to obtain an entirely closed form, it is necessary to do perform some analytic wizardry (see Watson 1939 for details). The fact that a closed form exists at all for this integral is therefore rather amazing.
REFERENCES:
Bailey, D. H.; Borwein, J. M.; Kapoor, V.; and Weisstein, E. W. "Ten Problems in Experimental Mathematics." Amer. Math. Monthly 113, 481-509, 2006b.
Borwein, J. and Bailey, D. Mathematics by Experiment: Plausible Reasoning in the 21st Century. Wellesley, MA: A K Peters, 2003.
Domb, C. "On Multiple Returns in the Random-Walk Problem." Proc. Cambridge Philos. Soc. 50, 586-591, 1954.
Glasser, M. L. and Zucker, I. J. "Extended Watson Integrals for the Cubic Lattices." Proc. Nat. Acad. Sci. U.S.A. 74, 1800-1801, 1977.
Joyce, G. and Zucker, I. J. "On the Evaluation of Generalized Watson Integrals." Proc. Amer. Math. Soc. 133, 71-81, 2005.
McCrea, W. H. and Whipple, F. J. W. "Random Paths in Two and Three Dimensions." Proc. Roy. Soc. Edinburgh 60, 281-298, 1940.
Sloane, N. J. A. Sequences A091670, A091671, and A091672 in "The On-Line Encyclopedia of Integer Sequences."
Watson G. N. "The Expansion of Products of Hypergeometric Functions." Quart. J. Pure Appl. Math. 39, 27-51, 1907.
Watson G. N. "A Series for the Square of the Hypergeometric Function." Quart. J. Pure Appl. Math. 40, 46-57, 1908.
Watson, G. N. "Three Triple Integrals." Quart. J. Math., Oxford Ser. 2 10, 266-276, 1939.
الاكثر قراءة في التفاضل و التكامل
اخر الاخبار
اخبار العتبة العباسية المقدسة
