Adiabatic changes
المؤلف:
Peter Atkins، Julio de Paula
المصدر:
ATKINS PHYSICAL CHEMISTRY
الجزء والصفحة:
ص47-48
2025-11-02
50
Adiabatic changes
We are now equipped to deal with the changes that occur when a perfect gas expands adiabatically. A decrease in temperature should be expected: because work is done but no heat enters the system, the internal energy falls, and therefore the temperature of the working gas also falls. In molecular terms, the kinetic energy of the molecules falls as work is done, so their average speed decreases, and hence the temperature falls. The change in internal energy of a perfect gas when the temperature is changed from Ti to Tf and the volume is changed from Vi to Vf can be expressed as the sum of two steps (Fig. 2.17). In the first step, only the volume changes and the temperature is held constant at its initial value. However, because the internal energy of a perfect gas is independent of the volume the molecules occupy, the overall change in internal energy arises solely from the second step, the change in temperature at constant volume. Provided the heat capacity is independent of temperature, this change is
∆U=CV(Tf−Ti)=CV∆T
Because the expansion is adiabatic, we know that q = 0; because ∆U = q + w, it then follows that ∆U = wad. The subscript ‘ad’ denotes an adiabatic process. Therefore, by equating the two values we have obtained for ∆U, we obtain
wad =CV∆T
That is, the work done during an adiabatic expansion of a perfect gas is proportional to the temperature difference between the initial and final states. That is exactly what we expect on molecular grounds, because the mean kinetic energy is proportional to T, so a change in internal energy arising from temperature alone is also expected to be proportional to ∆T. In Further information 2.1 we show that the initial and final temperatures of a perfect gas that undergoes reversible adiabatic expansion (reversible expansion in a thermally insulated container) can be calculated from
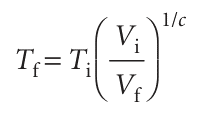
where c =CV,m/R, or equivalently
ViTic = VfTfc This result is often summarized in the form VTc = constant.
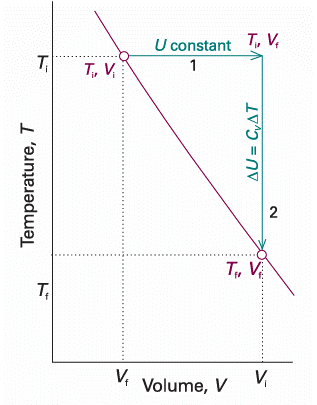
Fig. 2.17 To achieve a change of state from one temperature and volume to another temperature and volume, we may consider the overall change as composed of two steps. In the first step, the system expands at constant temperature; there is no change in internal energy if the system consists of a perfect gas. In the second step, the temperature of the system is reduced at constant volume. The overall change in internal energy is the sum of the changes for the two steps.
We also show in Further information 2.1 that the pressure of a perfect gas that undergoes reversible adiabatic expansion from a volume Vi to a volume Vf is related to its initial pressure by
pfVfγ = piViγ
where γ = Cp,m/CV,m. This result is summarized in the form pVγ = constant. For a monatomic perfect gas, CV, m= 3/2R (see Illustration 2.3), and from eqn 2.26 Cp,m = 5/2R; so γ = 5/3. For a gas of nonlinear polyatomic molecules (which can rotate as well as translate), CV,m = 3R, so γ = 4/3. The curves of pressure versus volume for adiabatic change are known as adiabats, and one for a reversible path is illustrated in Fig. 2.18. Because γ > 1, an adiabat falls more steeply (p ∝ 1/Vγ) than the corresponding isotherm (p ∝ 1/V). The physical reason for the difference is that, in an isothermal expansion, energy flows into the system as heat and maintains the temperature; as a result, the pressure does not fall as much as in an adiabatic expansion.
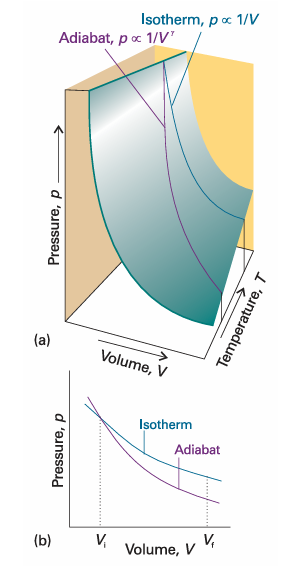
Fig. 2.18 An adiabat depicts the variation of pressure with volume when a gas expands adiabatically. (a) An adiabat for a perfect gas undergoing reversible expansion. (b) Note that the pressure declines more steeply for an adiabat than it does for an isotherm because the temperature decreases in the former.
الاكثر قراءة في مواضيع عامة في الكيمياء الفيزيائية
اخر الاخبار
اخبار العتبة العباسية المقدسة
