Heat capacity
المؤلف:
Peter Atkins، Julio de Paula
المصدر:
ATKINS PHYSICAL CHEMISTRY
الجزء والصفحة:
ص38-40
2025-11-02
42
Heat capacity
The internal energy of a substance increases when its temperature is raised. The increase depends on the conditions under which the heating takes place and for the present we suppose that the sample is confined to a constant volume. For example, the sample may be a gas in a container of fixed volume. If the internal energy is plotted against temperature, then a curve like that in Fig. 2.10 may be obtained. The slope of the tangent to the curve at any temperature is called the heat capacity of the system at that temperature. The heat capacity at constant volume is denoted CV and is defined formally as3
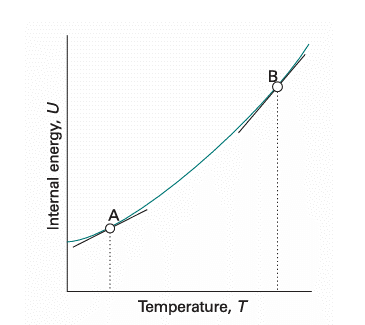
Fig. 2.10 The internal energy of a system increases as the temperature is raised; this graph shows its variation as the system is heated at constant volume. The slope of the tangent to the curve at any temperature is the heat capacity at constant volume at that temperature. Note that, for the system illustrated, the heat capacity is greater at B than at A.
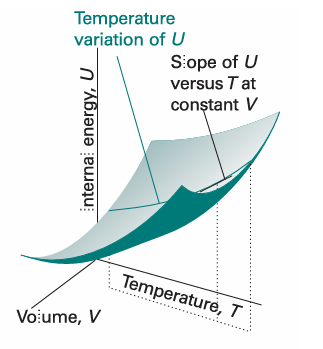
Fig. 2.11 The internal energy of a system varies with volume and temperature, perhaps as shown here by the surface. The variation of the internal energy with temperature at one particular constant volume is illustrated by the curve drawn parallel to T. The slope of this curve at any point is the partial derivative (∂U/∂T)V.
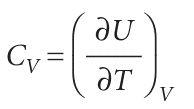
In this case, the internal energy varies with the temperature and the volume of the sample, but we are interested only in its variation with the temperature, the volume being held constant (Fig. 2.11).
Heat capacities are extensive properties: 100 g of water, for instance, has 100 times the heat capacity of 1 g of water (and therefore requires 100 times the energy as heat to bring about the same rise in temperature). The molar heat capacity at constant volume, CV, m = CV/n, is the heat capacity per mole of material, and is an intensive property (all molar quantities are intensive). Typical values of CV, m for polyatomic gases are close to 25 J K−1 mol−1. For certain applications it is useful to know the specific heat capacity (more informally, the ‘specific heat’) of a substance, which is the heat capacity of the sample divided by the mass, usually in grams: CV, s = CV/m. The specific heat capacity of water at room temperature is close to 4 J K−1 g−1. In general, heat capacities depend on the temperature and decrease at low temperatures. However, over small ranges of temperature at and above room temperature, the variation is quite small and for approximate calculations heat capacities can be treated as almost independent of temperature. The heat capacity is used to relate a change in internal energy to a change in temperature of a constant-volume system. It follows from eqn 2.15 that , dU=CVdT (at constant volume) , That is, at constant volume, an infinitesimal change in temperature brings about an infinitesimal change in internal energy, and the constant of proportionality is CV. If the heat capacity is independent of temperature over the range of temperatures of interest, a measurable change of temperature, ∆T, brings about a measurable increase in internal energy, ∆U, where , ∆U=CV∆T (at constant volume) , Because a change in internal energy can be identified with the heat supplied at constant volume (eqn 2.13b), the last equation can be written , qV =CV∆T , This relation provides a simple way of measuring the heat capacity of a sample: a measured quantity of energy is transferred as heat to the sample (electrically, for example), and the resulting increase in temperature is monitored. The ratio of the energy trans ferred as heat to the temperature rise it causes (qV/∆T) is the constant-volume heat capacity of the sample. , A large heat capacity implies that, for a given quantity of energy transferred as heat, there will be only a small increase in temperature (the sample has a large capacity for heat). An infinite heat capacity implies that there will be no increase in temperature however much energy is supplied as heat. At a phase transition, such as at the boiling point of water, the temperature of a substance does not rise as energy is supplied as heat: the energy is used to drive the endothermic transition, in this case to vaporize the water, rather than to increase its temperature. Therefore, at the temperature of a phase transition, the heat capacity of a sample is infinite. The properties of heat capacities close to phase transitions are treated more fully in Section 4.7.
الاكثر قراءة في مواضيع عامة في الكيمياء الفيزيائية
اخر الاخبار
اخبار العتبة العباسية المقدسة
