We now turn to our main topic of discussion: transients. By a transient is meant a solution of the differential equation when there is no force present, but when the system is not simply at rest. (Of course, if it is standing still at the origin with no force acting, that is a nice problem—it stays there!) Suppose the oscillation starts another way: say it was driven by a force for a while, and then we turn off the force. What happens then? Let us first get a rough idea of what will happen for a very high Q system. So long as a force is acting, the stored energy stays the same, and there is a certain amount of work done to maintain it. Now suppose we turn off the force, and no more work is being done; then the losses which are eating up the energy of the supply are no longer eating up its energy—there is no more driver. The losses will have to consume, so to speak, the energy that is stored. Let us suppose that Q/2π=1000. Then the work done per cycle is 1/1000 of the stored energy. Is it not reasonable, since it is oscillating with no driving force, that in one cycle the system will still lose a thousandth of its energy E, which ordinarily would have been supplied from the outside, and that it will continue oscillating, always losing 1/1000 of its energy per cycle? So, as a guess, for a relatively high Q system, we would suppose that the following equation might be roughly right (we will later do it exactly, and it will turn out that it was right!):

This is rough because it is true only for large Q. In each radian the system loses a fraction 1/Q of the stored energy E. Thus in a given amount of time dt the energy will change by an amount ωdt/Q, since the number of radians associated with the time dt is ωdt. What is the frequency? Let us suppose that the system moves so nicely, with hardly any force, that if we let go it will oscillate at essentially the same frequency all by itself. So we will guess that ω is the resonant frequency ω₀. Then we deduce from Eq. (24.8) that the stored energy will vary as

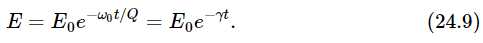
This would be the measure of the energy at any moment. What would the formula be, roughly, for the amplitude of the oscillation as a function of the time? The same? No! The amount of energy in a spring, say, goes as the square of the displacement; the kinetic energy goes as the square of the velocity; so, the total energy goes as the square of the displacement. Thus, the displacement, the amplitude of oscillation, will decrease half as fast because of the square. In other words, we guess that the solution for the damped transient motion will be an oscillation of frequency close to the resonance frequency ω₀, in which the amplitude of the sine-wave motion will diminish as e^−γt/2:

This equation and Fig. 24–1 give us an idea of what we should expect; now let us try to analyze the motion precisely by solving the differential equation of the motion itself.

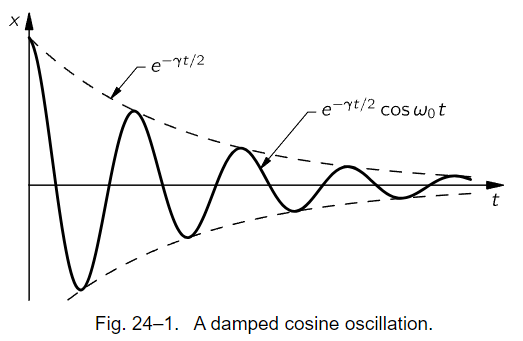
Fig. 24–1. A damped cosine oscillation.

So, starting with Eq. (24.1), with no outside force, how do we solve it? Being physicists, we do not have to worry about the method as much as we do about what the solution is. Armed with our previous experience, let us try as a solution an exponential curve, x=Ae^iαt. (Why do we try this? It is the easiest thing to differentiate!) We put this into (24.1) (with F(t)=0), using the rule that each time we differentiate x with respect to time, we multiply by iα. So it is really quite simple to substitute. Thus our equation looks like this:

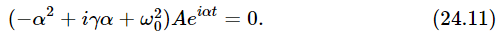
The net result must be zero for all times, which is impossible unless (a) A=0, which is no solution at all—it stands still, or (b)

If we can solve this and find an α, then we will have a solution in which A need not be zero!

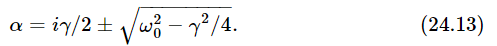
For a while we shall assume that γ is fairly small compared with ω₀, so that ω²₀−γ²/4 is definitely positive, and there is nothing the matter with taking the square root. The only bothersome thing is that we get two solutions! Thus

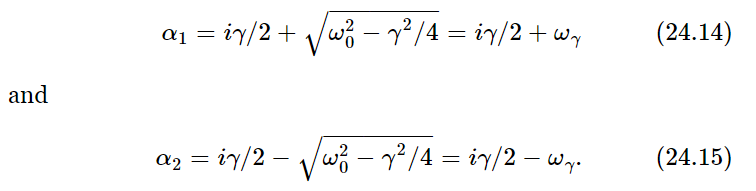
Let us consider the first one, supposing that we had not noticed that the square root has two possible values. Then we know that a solution for x is x₁=Ae^iα₁^t, where A is any constant whatever. Now, in substituting α₁, because it is going to come so many times and it takes so long to write, we shall call 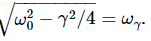. Thus iα₁=−γ/2+iω_γ, and we get x=Ae^(−γ/2+iω_γ^)t, or what is the same, because of the wonderful properties of an exponential,

First, we recognize this as an oscillation, an oscillation at a frequency ω_γ, which is not exactly the frequency ω₀, but is rather close to ω₀ if it is a good system. Second, the amplitude of the oscillation is decreasing exponentially! If we take, for instance, the real part of (24.16), we get

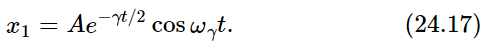
This is very much like our guessed-at solution (24.10), except that the frequency really is ω_γ. This is the only error, so it is the same thing—we have the right idea. But everything is not all right! What is not all right is that there is another solution.

The other solution is α₂, and we see that the difference is only that the sign of ω_γ is reversed:

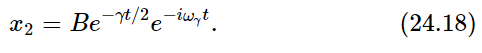
What does this mean? We shall soon prove that if x₁ and x₂ are each a possible solution of Eq. (24.1) with F=0, then x₁+x₂ is also a solution of the same equation! So, the general solution x is of the mathematical form

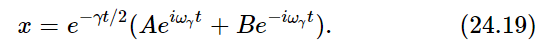
Now we may wonder why we bother to give this other solution, since we were so happy with the first one all by itself. What is the extra one for, because of course we know we should only take the real part? We know that we must take the real part, but how did the mathematics know that we only wanted the real part? When we had a nonzero driving force F(t), we put in an artificial force to go with it, and the imaginary part of the equation, so to speak, was driven in a definite way. But when we put F(t)≡0, our convention that x should be only the real part of whatever we write down is purely our own, and the mathematical equations do not know it yet. The physical world has a real solution, but the answer that we were so happy with before is not real, it is complex. The equation does not know that we are arbitrarily going to take the real part, so it has to present us, so to speak, with a complex conjugate type of solution, so that by putting them together we can make a truly real solution; that is what α₂ is doing for us. In order for x to be real, B e^−iωγt will have to be the complex conjugate of A e^iωγt that the imaginary parts disappear. So it turns out that B is the complex conjugate of A, and our real solution is

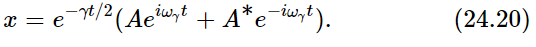
So our real solution is an oscillation with a phase shift and a damping—just as advertised.

مواضيع ذات صلة

The Doppler effect

Finding the “apparent” motion

Series and parallel impedances

Analogs in physics

Oscillations in linear systems

The energy of an oscillator

The forced oscillator with damping

Complex numbers and harmonic motion

Forced oscillations

Initial conditions for Harmonic motion and circular motion

Harmonic motion and circular motion

The harmonic oscillator