Complemented Lattice
المؤلف:
المرجع الالكتروني للمعلوماتيه
المصدر:
www.almerja.com
الجزء والصفحة:
...
31-12-2021
1986
Complemented Lattice
A complemented lattice is an algebraic structure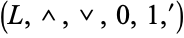 
such that 
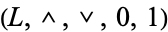is a bounded lattice and for each element 
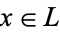, the element 
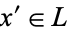is a complement of 
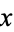, meaning that it satisfies
1. 
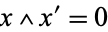
2. 
.
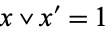A related notion is that of a lattice with complements. Such a structure is a bounded lattice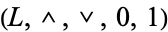 
such that for each 
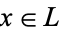, there is 
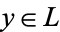such that 
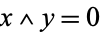and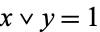 
.
One difference between these notions is that the class of complemented lattices forms a variety, whilst the class of lattices with complements does not. (The class of lattices with complements is a subclass of the variety of lattices, but it is not a subvariety of the class of lattices.) Every lattice with complements is a reduct of a complemented lattice, by the axiom of choice. To see this, let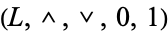 
be a lattice with complements. For each 
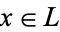, let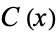 
denote the set of complements of 
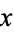. Because 
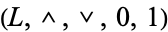is a lattice with complements, for each 
, 
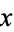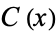is nonempty, so by the axiom of choice, we may choose from each collection 
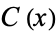a distinguished complement 
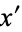for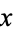 
. This defines a function 
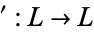which is a complementation operation, meaning that it satisfies the properties stated above for the complementation operation of a complemented lattice. Augmenting the bounded lattice 
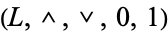with this operation yields a complemented lattice, 
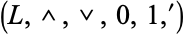of which the original lattice with complements 
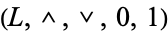is a reduct.
الاكثر قراءة في نظرية المجموعات
اخر الاخبار
اخبار العتبة العباسية المقدسة
