The logistic equation (sometimes called the Verhulst model or logistic growth curve) is a model of population growth first published by Pierre Verhulst (1845, 1847). The model is continuous in time, but a modification of the continuous equation to a discrete quadratic recurrence equation known as the logistic map is also widely used.

The continuous version of the logistic model is described by the differential equation

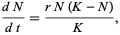(1)

where 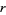 is the Malthusian parameter (rate of maximum population growth) and  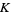is the so-called carrying capacity (i.e., the maximum sustainable population). Dividing both sides by  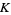and defining  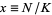then gives the differential equation

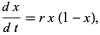(2)

which is known as the logistic equation and has solution

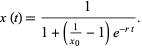(3)

The function 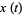 is sometimes known as the sigmoid function.

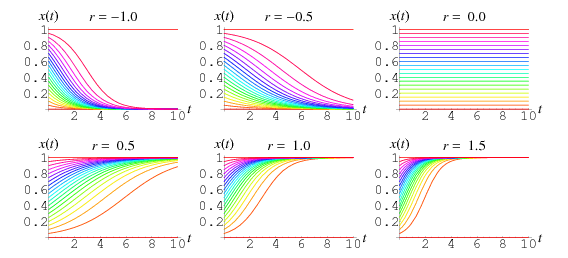
While 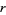 is usually constrained to be positive, plots of the above solution are shown for various positive and negative values of  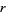and initial conditions  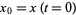ranging from 0.00 to 1.00 in steps of 0.05.

The discrete version of the logistic equation (3) is known as the logistic map.

The curve

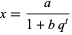(4)

obtained from (3) is sometimes known as the logistic curve. Similarly, a normalized form of equation (3) is commonly used as a statistical distribution known as the logistic distribution.

REFERENCES:

Verhulst, P.-F. "Recherches mathématiques sur la loi d'accroissement de la population." Nouv. mém. de l'Academie Royale des Sci. et Belles-Lettres de Bruxelles 18, 1-41, 1845.

Verhulst, P.-F. "Deuxième mémoire sur la loi d'accroissement de la population." Mém. de l'Academie Royale des Sci., des Lettres et des Beaux-Arts de Belgique 20, 1-32, 1847.

Wolfram, S. A New Kind of Science. Champaign, IL: Wolfram Media, p. 918, 2002.