Finite Difference
The finite difference is the discrete analog of the derivative. The finite forward difference of a function 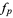 is defined as
is defined as
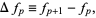 |
(1)
|
and the finite backward difference as
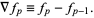 |
(2)
|
The forward finite difference is implemented in the Wolfram Language as DifferenceDelta[f, i].
If the values are tabulated at spacings 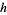 , then the notation
, then the notation
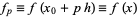 |
(3)
|
is used. The 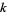 th forward difference would then be written as
th forward difference would then be written as 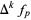 , and similarly, the
, and similarly, the 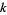 th backward difference as
th backward difference as 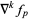 .
.
However, when 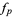 is viewed as a discretization of the continuous function
is viewed as a discretization of the continuous function 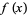 , then the finite difference is sometimes written
, then the finite difference is sometimes written
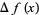 |
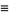 |
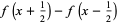 |
(4)
|
 |
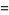 |
![2AdjustmentBox[I, BoxMargins -> <span style=]() {{0.101266, -0.101266}, {0.375, -0.375}}, BoxBaselineShift -> -0.375]AdjustmentBox[I, BoxMargins -> {{0, 0}, {-0.25, 0.25}}, BoxBaselineShift -> 0.25](x)*f(x)," src="https://mathworld.wolfram.com/images/equations/FiniteDifference/Inline14.gif" style="height:15px; width:85px" /> {{0.101266, -0.101266}, {0.375, -0.375}}, BoxBaselineShift -> -0.375]AdjustmentBox[I, BoxMargins -> {{0, 0}, {-0.25, 0.25}}, BoxBaselineShift -> 0.25](x)*f(x)," src="https://mathworld.wolfram.com/images/equations/FiniteDifference/Inline14.gif" style="height:15px; width:85px" /> |
(5)
|
where 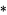 denotes convolution and
denotes convolution and ![AdjustmentBox[I, BoxMargins -> <span style=]() {{0.101266, -0.101266}, {0.375, -0.375}}, BoxBaselineShift -> -0.375]AdjustmentBox[I, BoxMargins -> {{0, 0}, {-0.25, 0.25}}, BoxBaselineShift -> 0.25](x)" src="https://mathworld.wolfram.com/images/equations/FiniteDifference/Inline16.gif" style="height:15px; width:33px" /> is the odd impulse pair. The finite difference operator can therefore be written
{{0.101266, -0.101266}, {0.375, -0.375}}, BoxBaselineShift -> -0.375]AdjustmentBox[I, BoxMargins -> {{0, 0}, {-0.25, 0.25}}, BoxBaselineShift -> 0.25](x)" src="https://mathworld.wolfram.com/images/equations/FiniteDifference/Inline16.gif" style="height:15px; width:33px" /> is the odd impulse pair. The finite difference operator can therefore be written
![Delta^~=2AdjustmentBox[I, BoxMargins -> <span style=]() {{0.101266, -0.101266}, {0.375, -0.375}}, BoxBaselineShift -> -0.375]AdjustmentBox[I, BoxMargins -> {{0, 0}, {-0.25, 0.25}}, BoxBaselineShift -> 0.25]*. " src="https://mathworld.wolfram.com/images/equations/FiniteDifference/NumberedEquation4.gif" style="height:18px; width:69px" /> {{0.101266, -0.101266}, {0.375, -0.375}}, BoxBaselineShift -> -0.375]AdjustmentBox[I, BoxMargins -> {{0, 0}, {-0.25, 0.25}}, BoxBaselineShift -> 0.25]*. " src="https://mathworld.wolfram.com/images/equations/FiniteDifference/NumberedEquation4.gif" style="height:18px; width:69px" /> |
(6)
|
An 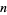 th power has a constant
th power has a constant 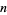 th finite difference. For example, take
th finite difference. For example, take 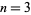 and make a difference table,
and make a difference table,
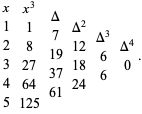 |
(7)
|
The 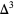 column is the constant 6.
column is the constant 6.
Finite difference formulas can be very useful for extrapolating a finite amount of data in an attempt to find the general term. Specifically, if a function 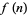 is known at only a few discrete values
is known at only a few discrete values 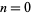 , 1, 2, ... and it is desired to determine the analytical form of
, 1, 2, ... and it is desired to determine the analytical form of 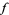 , the following procedure can be used if
, the following procedure can be used if 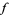 is assumed to be a polynomial function. Denote the
is assumed to be a polynomial function. Denote the 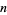 th value in the sequence of interest by
th value in the sequence of interest by 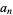 . Then define
. Then define 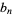 as the forward difference
as the forward difference 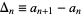 ,
, 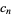 as the second forward difference
as the second forward difference 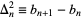 , etc., constructing a table as follows
, etc., constructing a table as follows
Continue computing 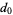 ,
, 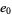 , etc., until a 0 value is obtained. Then the polynomial function giving the values
, etc., until a 0 value is obtained. Then the polynomial function giving the values 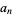 is given by
is given by
When the notation 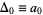 ,
, 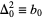 , etc., is used, this beautiful equation is called Newton's forward difference formula. To see a particular example, consider a sequence with first few values of 1, 19, 143, 607, 1789, 4211, and 8539. The difference table is then given by
, etc., is used, this beautiful equation is called Newton's forward difference formula. To see a particular example, consider a sequence with first few values of 1, 19, 143, 607, 1789, 4211, and 8539. The difference table is then given by
 |
(14)
|
Reading off the first number in each row gives 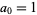 ,
, 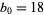 ,
, 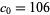 ,
, 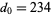 ,
, 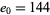 . Plugging these in gives the equation
. Plugging these in gives the equation
which indeed fits the original data exactly.
Formulas for the derivatives are given by
(Beyer 1987, pp. 449-451; Zwillinger 1995, p. 705).
Formulas for integrals of finite differences
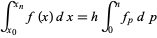 |
(28)
|
are given by Beyer (1987, pp. 455-456).
Finite differences lead to difference equations, finite analogs of differential equations. In fact, umbral calculus displays many elegant analogs of well-known identities for continuous functions. Common finite difference schemes for partial differential equations include the so-called Crank-Nicolson, Du Fort-Frankel, and Laasonen methods.
REFERENCES:
Abramowitz, M. and Stegun, I. A. (Eds.). "Differences." §25.1 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 877-878, 1972.
Beyer, W. H. CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, pp. 429-515, 1987.
Boole, G. and Moulton, J. F. A Treatise on the Calculus of Finite Differences, 2nd rev. ed. New York: Dover, 1960.
Conway, J. H. and Guy, R. K. "Newton's Useful Little Formula." In The Book of Numbers. New York: Springer-Verlag, pp. 81-83, 1996.
Fornberg, B. "Calculation of Weights in Finite Difference Formulas." SIAM Rev. 40, 685-691, 1998.
Iyanaga, S. and Kawada, Y. (Eds.). "Interpolation." Appendix A, Table 21 in Encyclopedic Dictionary of Mathematics. Cambridge, MA: MIT Press, pp. 1482-1483, 1980.
Jordan, C. Calculus of Finite Differences, 3rd ed. New York: Chelsea, 1965.
Levy, H. and Lessman, F. Finite Difference Equations. New York: Dover, 1992.
Milne-Thomson, L. M. The Calculus of Finite Differences. London: Macmillan, 1951.
Richardson, C. H. An Introduction to the Calculus of Finite Differences. New York: Van Nostrand, 1954.
Spiegel, M. Calculus of Finite Differences and Differential Equations. New York: McGraw-Hill, 1971.
Stirling, J. Methodus differentialis, sive tractatus de summation et interpolation serierum infinitarium. London, 1730. English translation by Holliday, J. The Differential Method: A Treatise of the Summation and Interpolation of Infinite Series. 1749.
Tweddle, C. James Stirling: A Sketch of His Life and Works Along with his Scientific Correspondence. Oxford, England: Oxford University Press, pp. 30-45, 1922.
Weisstein, E. W. "Books about Finite Difference Equations." http://www.ericweisstein.com/encyclopedias/books/FiniteDifferenceEquations.html.
Zwillinger, D. (Ed.). "Difference Equations" and "Numerical Differentiation." §3.9 and 8.3.2 in CRC Standard Mathematical Tables and Formulae. Boca Raton, FL: CRC Press, pp. 228-235 and 705-705, 1995.
 الاكثر قراءة في الرياضيات التطبيقية
الاكثر قراءة في الرياضيات التطبيقية
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


