Probability is the branch of mathematics that studies the possible outcomes of given events together with the outcomes' relative likelihoods and distributions. In common usage, the word "probability" is used to mean the chance that a particular event (or set of events) will occur expressed on a linear scale from 0 (impossibility) to 1 (certainty), also expressed as a percentage between 0 and 100%. The analysis of events governed by probability is called statistics.

There are several competing interpretations of the actual "meaning" of probabilities. Frequentists view probability simply as a measure of the frequency of outcomes (the more conventional interpretation), while Bayesians treat probability more subjectively as a statistical procedure that endeavors to estimate parameters of an underlying distribution based on the observed distribution.

A properly normalized function that assigns a probability "density" to each possible outcome within some interval is called a probability density function (or probability distribution function), and its cumulative value (integral for a continuous distribution or sum for a discrete distribution) is called a distribution function (or cumulative distribution function).

A variate is defined as the set of all random variables that obey a given probabilistic law. It is common practice to denote a variate with a capital letter (most commonly 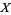). The set of all values that  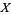can take is then called the range, denoted  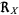(Evans et al. 2000, p. 5). Specific elements in the range of  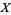are called quantiles and denoted , and the probability that a variate 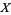 assumes the element  is denoted .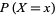

Probabilities are defined to obey certain assumptions, called the probability axioms. Let a sample space contain the union (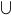) of all possible events 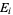, so

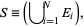(1)

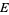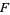and let  and  denote subsets of 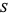. Further, let  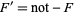be the complement of 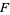, so that

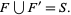(2)

Then the set 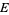 can be written as

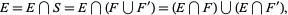(3)

where 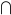 denotes the intersection. Then

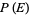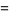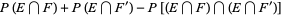			(4)
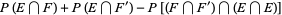			(5)
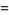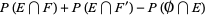			(6)
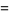			(7)
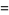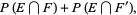			(8)

where 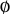 is the empty set.

Let 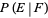 denote the conditional probability of  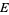given that  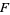has already occurred, then

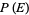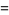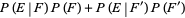			(9)
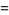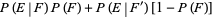			(10)
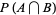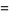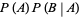			(11)
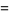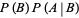			(12)
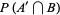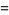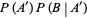			(13)
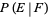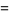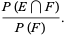			(14)

The relationship

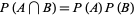(15)

holds if 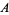 and 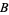 are independent events. A very important result states that

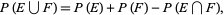(16)

which can be generalized to

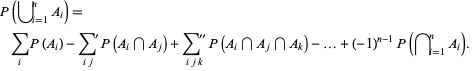(17)

REFERENCES:

Evans, M.; Hastings, N.; and Peacock, B. Statistical Distributions, 3rd ed. New York: Wiley, 2000.

Everitt, B. Chance Rules: An Informal Guide to Probability, Risk, and Statistics. Copernicus, 1999.

Goldberg, S. Probability: An Introduction. New York: Dover, 1986.

Keynes, J. M. A Treatise on Probability. London: Macmillan, 1921.

Mises, R. von Mathematical Theory of Probability and Statistics. New York: Academic Press, 1964.

Mises, R. von Probability, Statistics, and Truth, 2nd rev. English ed. New York: Dover, 1981.

Mosteller, F. Fifty Challenging Problems in Probability with Solutions. New York: Dover, 1987.

Mosteller, F.; Rourke, R. E. K.; and Thomas, G. B. Probability: A First Course, 2nd ed. Reading, MA: Addison-Wesley, 1970.

Nahin, P. J. Duelling Idiots and Other Probability Puzzlers. Princeton, NJ: Princeton University Press, 2000.

Neyman, J. First Course in Probability and Statistics. New York: Holt, 1950.

Rényi, A. Foundations of Probability. San Francisco, CA: Holden-Day, 1970.

Ross, S. M. A First Course in Probability, 5th ed. Englewood Cliffs, NJ: Prentice-Hall, 1997.

Ross, S. M. Introduction to Probability and Statistics for Engineers and Scientists. New York: Wiley, 1987.

Ross, S. M. Applied Probability Models with Optimization Applications. New York: Dover, 1992.

Ross, S. M. Introduction to Probability Models, 6th ed. New York: Academic Press, 1997.

Székely, G. J. Paradoxes in Probability Theory and Mathematical Statistics, rev. ed. Dordrecht, Netherlands: Reidel, 1986.

Todhunter, I. A History of the Mathematical Theory of Probability from the Time of Pascal to that of Laplace. New York: Chelsea, 1949.

Weaver, W. Lady Luck: The Theory of Probability. New York: Dover, 1963.

اخر الاخبار

اخبار العتبة العباسية المقدسة

دار الكفيل تنهي طباعة كتاب (لمَ لا) تمهيدًا لمناقشته في ملتقى غيث السماء القرآني الثاني

العتبة العباسية المقدسة تطلق مسابقتها الثقافية بذكرى ولادة الإمام زين العابدين (عليه السلام)

العتبة العباسية المقدسة تكرّم 1000 طالبة من المرتديات العباءة العراقية في مدارس الديوانية

العتبة العباسية المقدسة تؤكد أهمية الحجاب كجزء من منظومة الواجبات الشرعية

المزيد

الآخبار الصحية

الخبز الأسمر أم الأبيض.. أيهما أفضل لضبط سكر الدم؟

عقاقير التخسيس و"الانتحار".. الحكومة الأميركية تحسم الجدل

الهرم الغذائي الجديد.. لماذا يعد "انقلابا" في خارطة الطعام؟

لحماية ظهرك وقلبك في آن واحد.. ما وضعية النوم الصحيحة؟

المزيد

الآخبار التكنلوجية

كيف يعزز الضوء الطبيعي تفكيرك وانتباهك خلال اليوم

سابقة.. طاقم من محطة الفضاء الدولية يعود إلى الأرض مبكرا

منصات التواصل تضرّ بنفسية المراهقين… والفتيات الأكثر تأثرا

ابتكار ألماني قد يغيّر مستقبل صناعة البلاستيك

المزيد